Теплоты
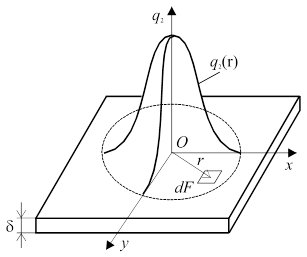
а) Мгновенный нормально-круговой источник на поверхности пластины. Рассмотрим характер распределения температур в пластине после введения теплоты мгновенным источником, который действовал время dt. Мгновенно на площадку dF источником вводится теплота (рис. 29):
Если принять, что температура по толщине пластины d быстро выравнивается, то мгновенное повышение температуры элемента объема dF×d составляет:
Из формулы (73) следует, что при действии мгновенного нормально-кругового источника температура распределяется по нормальному закону.
Как указывалось в § 1, гл. 5, подобное распределение температур наблюдается и при действии мгновенного линейного источника теплоты. Очевидно, можно подобрать такой линейный источник Q 1, который бы спустя время t 0 от начала своего действия привел бы к такому же распределению температур, какое вызывает нагрев мгновенным нормально-круговым источникам. Таким образом, мгновенный нормально-круговой источник можно заменить фиктивным мгновенным линейным источником. Определим параметры этого фиктивного источника:
Указанное равенство выполняется при следующих условиях: 1) 2) Учитывая, что Таким образом, фиктивный линейный источник имеет такую же мощность, что и нормально-круговой, и вводится на время t 0 раньше действительного номально-кругового источника. Процесс выравнивания температуры (t>;0) от действия мгновенного нормально-кругового источника определяется уравнением:
В момент приложения этого источника (t =0):
С учетом теплоотдачи в течение времени t температура в пластине определяется по формуле:
б ) Мгновенный нормально-круговой источник на поверхности полубесконечного тела. Нагрев полубесконечного тела мгновенным нормально-круговым источником рассматривается по аналогии с предыдущим случаем (§1-а) как процесс распространения теплоты от мгновенного точечного источника по поверхности полубесконечного тела. При этом принимается, что в течение времени t 0 теплота распространяется только по поверхности тела, а затем (t>t 0 ) начинает распространяться вглубь тела. В этом случае температурное поле определяется уравнением:
|

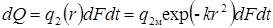 .
.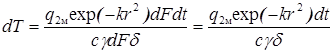 . (73)
. (73) .
. - постоянная времени нормально-кругового источника.
- постоянная времени нормально-кругового источника. .
. и
и  , получаем:
, получаем: 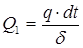 .
.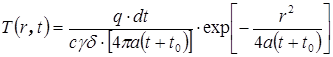 .
.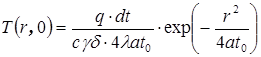 .
.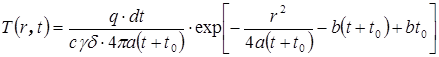 .
.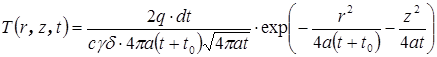 .
.


