Мгновенные сосредоточенные источники теплоты
а) Мгновенный точечный источник на поверхности полубесконечного тела. В точку 0 на поверхности полубесконечного тела (рис. 18-а) в начальный момент t= 0 введено количество теплоты Q Дж. Начальную температуру тела примем равной нулю. Граница тела хОу не пропускает теплоты, т.е. при z= 0 градиент ¶ T/¶z= 0. Теплоотдачей в окружающую среду с поверхности полубесконечного тела пренебрегают потому, что на температурное поле основное влияние оказывает распространение теплоты в глубь тела путем теплопроводности. Уравнение температурного поля мгновенного точечного источника Q на поверхности полубесконечного тела аналогично уравнению температурного поля (46) мгновенного точечного источника 2 Q в неограниченном теле:
Действительно, в случае неограниченного тела плоскость хОу также можно считать адиабатической, т. к. при действии точечного источника изотермическими поверхностями являются сферы с центром в точке 0, и при z= 0, градиент ¶ T/¶z= 0. Поэтому неограниченное тело с точечным источником 2 Q можно представить составленным из двух полубесконечных тел, на поверхности которых действуют точечные источники Q. Из уравнения (61) следует, что все точки на полусфере с постоянным радиусом R имеют в данный момент времени одинаковую температуру, т.е. температурное поле симметрично относительно точки 0. Изотермическими поверхностями являются полусферы с центром 0. Температура в любой точке тела прямо пропорциональна количеству введенной теплоты Q. Распределение температуры по радиусу-вектору R описывается нормальным законом распределения вероятностей. Кривизна распределения (рис. 20-а) зависит от значения времени t. а) б) Рис. 20. Процесс распространения теплоты мгновенного точечного источника в полубесконечном теле (Q =2000 Дж, cg= 40 Дж/см3K, а= 0,1 см2/с).
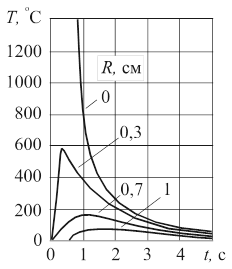
В начале процесса кривые распределения температуры высокие и крутые. В начальный момент времени кривая совпадает с осью ординат. По мере распространения теплоты температурные кривые становятся более пологими и температура выравнивается, стремясь к нулю. Рассмотрим как изменяется температура точек тела во времени (рис. 20-б). В начальный момент t =0 температура всех точек тела, кроме точки 0 (R =0), равна нулю. По мере распространения теплоты мгновенного точечного источника температуры точек тела повышаются, достигают наибольшего значения, а затем убывают, стремясь к нулю. Чем ближе к источнику расположена точка тела, тем раньше начинает возрастать ее температура, тем быстрее она растет и тем выше ее наибольшее значение. С течением времени температуры различных точек тела сближаются и стремятся к нулю. б) Мгновенный линейный источник в пластине. К линейному элементу 00' пластины (рис. 18-в) толщиной d приложен в момент времени t =0 мгновенный линейный источник Q с линейной интенсивностью Q1 = Q / d Дж/см. Если верхняя и нижняя плоскости пластины не пропускают теплоты, то температура в любой точке пластины будет оставаться одинаковой по толщине, и уравнение температурного поля будет аналогичным уравнению (47) температурного поля мгновенного линейного источника в неограниченном теле. Если же учитывать теплообмен пластины с окружающей средой, то температура по толщине пластины окажется неодинаковой - будет понижаться в направлении к наружным слоям пластины. Однако, при малой толщине пластины эта неравномерность температуры незначительна и ею пренебрегают, считая температуру осредненной по толщине. При этом влияние теплоотдачи учитывают следующим образом. Пусть на поверхностях пластины имеется теплоотдача с коэффициентом a в окружающую среду с нулевой температурой. Тогда каждый элементарный объем пластины ddxdy (рис. 21), нагретый до температуры T отдает за время dt в окружающую среду через обе поверхности пластины количество теплоты:
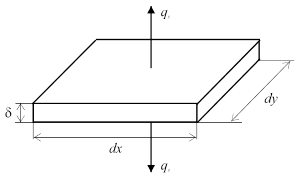
Мгновенное понижение температуры за счет теплоотдачи равно:
Выражая скорость охлаждения dT/dt, получаем:
где Дифференциальное уравнение теплопроводности для пластины с теплоотдачей имеет вид:
Оно отличается от уравнения Фурье для плоского поля (23) слагаемым (-bT), которое учитывает влияние теплоотдачи на скорость изменения температуры ¶T/¶t в любой точке пластины. Температурное поле мгновенного линейного источника в пластине с теплоотдачей является решением уравнения (62) и имеет вид:
где Оно отличается от уравнения (47) множителем e- bt, учитывающим теплоотдачу с поверхности пластины. Таким образом, значение теплоотдачи возрастает с увеличением времени процесса t и коэффициента температуроотдачи b, т. е. с уменьшением толщины пластины d, объемной теплоемкости су и с увеличением коэффициента теплоотдачи a. Температурное поле (63) симметрично относительно оси Oz, т.е. изотермическими поверхностями являются круговые цилиндры с осью Oz. Качественно процесс распространения теплоты в пластине протекает так же, как и в полубесконечном теле. Вдоль радиуса вектора r температура распределена по нормальному закону. Крутизна температурных кривых уменьшается с увеличением времени. Однако, время t входит в уравнение (63) в первой степени, а в уравнение (61) в степени 3/2. Поэтому процесс распространения теплоты в пластине замедлен по сравнению с процессом в полубесконечном теле. Это связано с тем, что поток теплоты в пластине стеснен ограничивающими ее плоскостями. в) Мгновенный плоский источник в стержне. В сечении x =0 неограниченного стержня (рис. 18-г) в момент t= 0 приложен мгновенный плоский источник Q, распределенный равномерно по сечению стержня с поверхностной интенсивностью Q 2= Q/F Дж/см2, где F— площадь сечения стержня. Если боковая поверхность стержня не пропускает теплоты, то температура в любом сечении стержня будет одинаковой по всему сечению, и уравнение температурного поля будет аналогичным уравнению (48) температурного поля мгновенного плоского источника в неограниченном теле. При наличии теплоотдачи с поверхности стержня температура в любом его сечении распределена неравномерно. Однако, при небольшой величине F принимают, что температура практически выравнена по поперечному сечению стержня. Тогда теплоотдачу с поверхности стержня учитывают так же, как и с поверхности пластины. Для стержня коэффициент температуроотдачи:
где р - периметр поперечного сечения стержня. Дифференциальное уравнение теплопроводности для стержня с теплоотдачей имеет вид:
Температурное поле мгновенного плоского источника в стержне с теплоотдачей является решением уравнения (64):
т.е. теплоотдача с поверхности стержня также учитывается множителем e- bt. Влияние теплоотдачи возрастает с увеличением времени процесса t, коэффициента теплоотдачи a, периметра сечения р и с уменьшением площади сечения F и объемной теплоемкости су. Температурное поле (65) является линейным и симметричным относительно плоскости х= 0. Качественно процесс распространения теплоты в стержне похож на процессы в полубесконечном теле и в пластине. По оси Ох температура распределена по нормальному закону. Тепловой поток в стержне еще более стеснен по сравнению с пластиной и полубесконечным телом. Поэтому процесс изменения температуры во времени в стержне происходит еще медленнее, чем в пластине.
|

 . (61)
. (61)
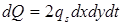 .
.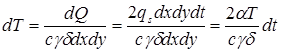 .
.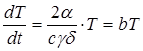 ,
,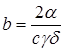 - коэффициент температуроотдачи, с-1.
- коэффициент температуроотдачи, с-1.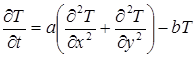 . (62)
. (62) , (63)
, (63)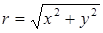 - расстояние от источника.
- расстояние от источника. ,
, . (64)
. (64) , (65)
, (65)


