для 1 курса РФФ
Литература 1. Ильин В.А., Позняк Э.Г. Линейная алгебра 2. Головина Л.И. Линейная алгебра и некоторые её приложения. 3. Мадунц А.И. Линейная алгебра
1. Пространство 2. Ранг матрицы: определение, формулировка теоремы о сохранении ранга при элементарных преобразова- ниях матрицы. Базисный минор матрицы, теорема о базисном миноре, её следствие. 3. Система линейных алгебраических уравнений, её запись в скалярной, матричной и векторной формах. Решение системы. Эквивалентные системы. Элементарные преобразования системы уравнений. Теорема Крамера, пример применения. 4. Однородная система, теорема о существовании ненулевых решений, её следствие. Лемма о линейной зави- симости линейных комбинаций n-мерных векторов. Базисный минор системы, базисные и свободные не- известные.Теорема о подсистеме базисных уравнений. Теорема о существовании и единственности реше- ния с заданным набором значений свободных неизвестных, её следствие. Теорема о структуре множества решений однородной системы. ФСР системы, общее решение однородной системы, его запись в скаляр- ной, матричной и векторной формах. 5. Неоднородная система линейных уравнений, теорема Кронекера-Капелли. Соответствующая однородная система, теорема о структуре множества решений неоднородной системы. Общее решение неоднородной системы, его запись в скалярной, матричной и векторной формах. Отыскание общего рещения системы методом Гаусса-Жордана, пример. 6. Линейное пространство (вещественное, комплексное): аксиомы, примеры. Следствия из аксиом. Задача. На заданном множестве определены две операции; вы я снить, является ли это множество линей- ным пространством. 7. Линейно зависимые системы: определение, примеры, свойства. Лемма о линейной зависимости линейных комбинаций элементов пространства. Линейно независимые системы: определение, примеры. Задача. Выяснить, является ли заданная система линейно зависимой или линeйно независимой. 8. Конечномерное линейное пространство: определение, примеры конечномерных пространств. Бесконечно- -мерные пространства, пример. Базис конечномерного пространства: определение, примеры. Теорема о существовании базиса конечномерного пространства, её следствие. Теорема о дополнении линейно неза- висимой системы до базиса. Задача. Задано линейное пространство и некоторая система его элементов; выяснить, является ли она базисом пространства. 9. Координаты вектора относительно заданного базиса, их единственность. Координатный вектор элемента линейного пространства свойства координатных векторов. 10. Матрица перехода от базиса к базису, её свойства. Преобразование координат при изменении базиса, пример. Задачи. 1) Найти координаты заданного вектора в заданном базисе. 2) Заданы две системы векторов; показать, что каждая из них является базисом, записать матрицу перехода от первого базиса ко второ- му. 3) Заданы два базиса и координаты вектора х в одном из этих базисов; найти координаты х в другом базисе. 11. Линейное множество (линейное подпространство): определение, примеры. Линейная оболочка системы векторов, примеры. Задача. Задана некоторая система векторов; определить размерность её линейной оболочки и указать её базис. 12. Линейное преобразование пространства (линейный оператор): определение, примеры. Матрица линейного оператора в заданном базисе, примеры. Теорема о матричном представлении линейного оператора. Дейст- вия над линейными операторами: определения, теорема о действиях над линейными операторами и их матрицами. Задачи. 1) Задано отображение линейного пространства в себя; выяснить, является ли оно линейным пре- образованием. 2) Записать матрицу заданного линейного оператора в указанном базисе. 3) Задана матрица оператора А в некотором базисе; известны координаты вектора х в том же базисе; найти Ах. 13. Образ и ядро линейного оператора: определения, примеры, лемма. Ранг и дефект линейного оператора, теорема о ранге и дефекте. Задачи. 1) Найти образ и ядро заданного оператора. 2) Найти ранг и дефект заданного оператора. 3) Пост-роить базисы образа оператора и его ядра. 14. Невырожденный оператор: определение, свойства. Обратный оператор: определение, свойства, пример. Задача. Задан оператор. Выяснить, существует ли обратный оператор и, если существует, найти матрицу обратного оператора в указанном базисе. 13. Преобразование матрицы линейного оператора при изменении базиса. Подобные матрицы: определение, свойства, теорема о подобной матрице. Задача. Известна матрица оператора в старом базисе; найти его матрицу в новом базисе. 14. Собственные числа и собственные векторы линейного оператора: определение, примеры, свойства. Характеристический многочлен матрицы, теорема о характеристических многочленах подобных матриц. Характеристический многочлен и характеристическое уравнение линейного оператора, теорема о корнях характеристического уравнения линейного оператора, её следствие. Собственное подпространство, приме- ры, геометрическая кратность собственного числа. 15. Необходимое и достаточное условие, при выполнении которого матрица оператора является диагональной. Оператор простой структуры: определение, два достаточных признака оператора простой структуры. Задачи. 1) Найти собственные числа и собственные векторы заданного оператора. 2) Определить геомет- рическую кратность собственного числа и построить базис принадлежащего ему собственного подпрост- ранства. 3) Выяснить, является ли заданный оператор оператором простой структуры; если да, то постро- ить базис пространства из собственных векторов оператора и записать матрицу оператора в этом базисе. 16. Скалярное произведение в вещественном линейном пространстве: определение, примеры. Норма элемента эвклидова пространства: определение, примеры, свойства. Ортогональные системы векторов: определение, примеры, теорема о линейной независимости ортогональной системы. Матрица Грама системы, её свойст- ва. Процесс Грама - Шмидта ортогонализации линейно независимой системы. Ортонормированные систе- мы: определение, свойства. Ортонормированные базисы: определение, примеры, свойства. Теорема о до- полнении ОНС до ОНБ Задачи. 1) Построить матрицу Грама заданной системы векторов. 2) Ортогонализовать заданную линейно независимую систему. 3) Известна матрица Грама базиса пространства; найти скалярное произведение за- данных векторов. 4) Найти матрицу Грама нового базиса, зная матрицу Грама старого базиса.5) Постро- ить ОНБ пространства. 17. Ортогональное дополнение линейного подпространства: определение, примеры, свойства. Задача Найти ортогональное дополнение (найти базис ортогонального дополнения), заданного линей- ного подпространства. 18. Сопряженный оператор: определение, теорема о существовании и единственности сопряженного операто- ра, свойства.. Задача. Найти матрицу оператора, сопряженного к заданному оператору. 19. Самосопряженный оператор: определение, пример, теоремы о матрице самосопряженного оператора, о действиях над самосопряженными операторами, об ортогональности собственных векторов самосопря- женного оператора. о корнях его характеристического уравнения, её следствие. 20. Инвариантное подпространство линейного оператора: определение, пример, свойства. Теорема о сущест- вовании ОНБ из собственных векторов самосопряженного оператора, её следствие. Задачи. 1)Выяснить, является ли заданный линейный оператор самосопряженным. 2)Построить ОНБ из собственных векторов самосопряженного оператора, записать матрицу оператора в этом базисе. 21. Ортогональная матрица: определение, свойства. Ортогональный оператор: определение, пример, свойства. Геометрический смысл ортогонального оператора в пространстве V2. 22. Квадратичная форма от n переменных. её матричное представление. Теорема о преобразовании матрицы квадратичной формы при линейном преобразовании переменных, её следствия. Приведение квадратичной формы к каноническому виду методом Лагранжа. Приведение квадратичной формы к каноническому виду ортогональным преобразованием переменных. Приведение уравнения поверхности второго порядка к каноническому виду. Закон инерции квадратичных форм. Положительный и отрицательный индекс инер- ции формы, её сигнатура. Классификация квадратичных форм. Теорема о классификации квадратичной формы с помощью индексов инерции. Формулировка критерия Сильвестра. Его следствие. Задачи. 1) Квадратичную форму привести к каноническому виду методом Лагранжа или ортогональным преобразованием, записать итоговое преобразование переменных, приводящее форму к каноническому виду, построить канонический базис. 2) Упростить уравнение поверхности второго порядка, сделать схема- тический чертеж поверхности в исходной системе координат. 3) Классифицировать заданную квадратич- ную форму с помощью критерия Сильвестра или с помощью индексов инерции.
28.
|

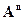 : n- мерный вектор, его координаты; сложение n – мерных векторов, умножение n – мер- ного вектора на число. Линейно зависимые и линейно независимые системы в
: n- мерный вектор, его координаты; сложение n – мерных векторов, умножение n – мер- ного вектора на число. Линейно зависимые и линейно независимые системы в 


