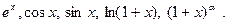Программа экзамена по математическому анализу
для 1 курса РФФ ( Литература 1. Кудрявцев Л.Д Курс математического анализа, т.т. 1,2 2. Аксёнов А.П. Математический анализ, части 1 и 2. 3. Рыжаков И.Ю. Определенный интеграл. Несобственные интегралы. 4. Рыжаков И.Ю. Ряды. Ряды Фурье.
1. Первообразная: определение, примеры, свойства. Неопределенный интеграл: определение, примеры, свой- ства. Табличные интегралы. Теорема о замене переменной под знаком неопределенного интеграла. Форму- ла интегрирования по частям. Интегрирование элементарных рациональных дробей. Интегрирование рацио нальных дробей. Метод рационализующих подстановок; подстановки Чебышева. 2. Площадь плоской фигуры: аксиомы, следствия из аксиом. 3. Лемма о точных гранях ограниченный функции. 4. Положительная и отрицательная части функции, их свойства. 5. Интегральные суммы: определения, геометрический смысл для неотрицательных функций, свойства. 6. Интегрируемые функции: определение, пример. Свойства интегрируемых функций. 7. Определенный интеграл: определение, пример, свойства, выражаемые равенствами, свойства, выражаемые неравенствами, теоремы о среднем. 8. Определенный интеграл с переменным верхним пределом: определение, теоремы о непрерывности, о диф- ференцируемости. Интеграл с переменным нижним пределом. 9. Теоремы Ньютона-Лейбница, о замене переменной под знаком определенного интеграла, формула интегри- рования по частям. 10. Несобственные интегралы по [a,b), по (a,b], по (a,b): определения, примеры., свойства. Формулировка тео- ремы о замене переменной под знаком несобственного интеграла. 11. Главное значение несобственного интеграла по интервалу: определение, пример. 12. Вычисление площади плоской фигуры в декартовой системе координат, пример. 13. Вычислнние площади плоской фигуры полярной системе координат, пример. 14. Формулировка теоремы о вычислении обьёма тела по его поперечным сечениям. Теорема о вычислении обьёма тела вращения, пример 15. Теорема о переменной длине дуги. Вычисление длины кривой, пример. 16. Сходящиеся и расходящиеся числовые ряды: определения, примеры. Общие свойства числовых рядов 17. Критерий сходимости ряда с неотрицательными членами. Интегральный признак Коши, его применение к исследованию обобщенного гармонического ряда. Первый и второй признаки сравнения. Признак Далам- бера, метод выделения главной части в исследовании ряда. Радикальный признак Коши. 18. Критерий Коши, его применение к исследованию гармонического ряда. Признак Лейбница, его применение к исследованию ряда 19. Абсолютная и условная сходимость числового ряда: определения, исследование рядов 20. Степенные ряды: определение, примеры, теорема Абеля. Теоремы о множестве сходимости ряда, о вычислении радиуса сходимости ряда. 21. Последовательность функций: множество её сходимости, её предельная функция, равномерная сходимость на множестве (определения и примеры). Теоремы о непрерывности предельной функции и о предельном переходе под знаком интеграла. 22. Функциональный ряд: множество его сходимости, сумма ряда, равномерная сходимость на множестве (определения и примеры). Признак Вейерштрасса равномерной сходимости ряда. Теоремы о непрерыв -ности суммы ряда, о почленном интегрировании, о почленном дифференцировании функциональных рядов. 23. Вещественный степенной ряд, теоремы о его равномерной сходимости внутри интервала сходимости, о почленном интегрировании, о почленном дифференцировании, о сохранении радиуса сходимости при почленном дифференцировании и почленном интегрировании ряда, о коэффициентах степенного ряда. 24. Коэффициенты Тейлора и ряд Тейлора. Теорема о достаточном условии разложимости функции в ряд Тейлора. Разложения в ряды Маклорена функций 25. Абсолютно интегрируемые функции: определения для различных случаев, признак Вейерштрасса абсо- лютной интегрируемости функции. 26. Тригонометрический многочлен. Тригонометрический ряд, теорема о коэффициентах равномерно сходящегося тригонометрического ряда. 27. Коэффициенты Фурье и ряд Фурье абсолютно интегрируемой функции. Формулировки трех теорем о достаточных условиях разложимости функции в ряд Фурье. Теорема о почленном интегрировании ряда Фурье. Ряд Фурье для произвольного промежутка. Функция с интегрируемым квадратом, её абсолютная интегрируемость. Минимальное свойство коэффициентов ряда Фурье. Неравенство Бесселя. Формулировка теоремы Вейерштрасса о равномерном приближении непрерывной функции тригонометрическими много- членами. Равенство Парсеваля.
|
семестр)
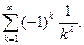Признак Дирихле, исследование ряда 
.
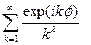на абсолютную и условную сходимость. Формулировки теорем о свойствах абсолютно сходящихся рядов: о произведении ряда на число, о сумме рядов. Формулировки теоремы Римана об условно сходящихся рядах. Формулировки теорем о переместительном свойстве абсолютно сходящихся рядов, о произведении абсолютно сходящихся рядов.
