Характеристики варіації
Для вимірювання та оцінки варіації використовують абсолютні та відносні характеристики. До абсолютних належать: розмах варіації (варіаційний розмах), середнє лінійне відхилення, середнє квадратичне відхилення, дисперсії; до відносних – коефіцієнти варіації, нерівномірності, локалізації, концентрації. Розмах варіації (R) характеризує діапазон варіації ознаки і являє собою різницю між максимальним (xmax) і мінімальним (xmin) значеннями ознаки: R = xmax - xmin. Оскільки розмах варіації визначається на основі тільки двох крайніх значень ознак сукупності, він дає уявлення про загальний розмір варіації і не дозволяє встановити рівень варіації всередині сукупності. З цієї причини його використовують для попередньої наближеної оцінки варіації. Більш точними показниками варіації є середнє лінійне відхилення ( Для згрупованих даних
За первинними не згрупованими даними зазначені характеристики варіації визначаються за принципом простої середньої:
Середнє лінійне і середнє квадратичне відхилення за змістом ідентичні, через математичні властивості Дисперсія – це середній квадрат відхилень
Для альтернативної ознаки, варіація якої має два взаємовиключні значення – “1” (наявність) та “0” (відсутність), а розподіл характеризується відповідно двома частками – p і q (p + q =1, звідки p =1- q, q =1- p), дисперсія обчислюється як добуток часток При статистичному аналізі варіацій різних ознак або порівнянні варіації однієї і тієї ж ознаки в різних сукупностях використовують відносні характеристики варіації. Коефіцієнти варіації визначають відношенням абсолютних характеристик варіації (R, осциляції квадратичний Чим більшою є величина коефіцієнта варіації, тим більшим є розшарування значень ознаки навколо середньої величини, тим більша неоднорідність сукупності. Квадратичний коефіцієнт варіації
|

 ) та середнє квадратичне відхилення (
) та середнє квадратичне відхилення (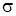 ), які ґрунтуються на відхиленні всіх індивідуальних значень ознаки від середньої величини (
), які ґрунтуються на відхиленні всіх індивідуальних значень ознаки від середньої величини ( ). Оскільки алгебраїчна сума відхилень
). Оскільки алгебраїчна сума відхилень  =0, то використовують або модулі
=0, то використовують або модулі  , або квадрати
, або квадрати 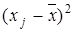 відхилень. Середнє лінійне відхилення і середнє квадратичне відхилення є іменованими величинами і визначаються в одиницях вимірювання ознаки.
відхилень. Середнє лінійне відхилення і середнє квадратичне відхилення є іменованими величинами і визначаються в одиницях вимірювання ознаки. ;
; 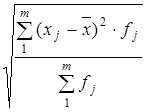 .
. ;
; 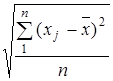 .
.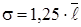 , R =
, R =  .
.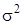 . Застосування дисперсії більш широке, ніж тільки для оцінки варіації. Так, її використовують і при вимірюванні взаємозв`язків. Для ознак метричної шкали визначення дисперсії проводиться за такими формулами:
. Застосування дисперсії більш широке, ніж тільки для оцінки варіації. Так, її використовують і при вимірюванні взаємозв`язків. Для ознак метричної шкали визначення дисперсії проводиться за такими формулами:
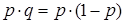 .
.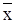 ) і найчастіше виражаються у відсотках:
) і найчастіше виражаються у відсотках: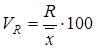 ; лінійний
; лінійний 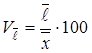 ;
;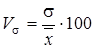 .
. використовують як критерій однорідності сукупності. Вважається, що при значенні
використовують як критерій однорідності сукупності. Вважається, що при значенні  сукупність є однорідною, а
сукупність є однорідною, а 


