Розв`язок типових задач
Задача 1. Визначимо середній, модальний і медіанний вік студентів за даними вищенаведеної таблиці про розподіл студентів-заочників однієї групи (табл.1). Розв`язок задачі. Для розрахунку зазначених характеристик центру розподілу побудуємо табл.2. Таблиця 2. Розподіл студентів за віком
Перший інтервал (відкритий) умовно прирівнюємо по ширині до другого (закритого), а останній (відкритий) - до передостаннього (закритого). Так, якщо ширина другого інтервалу 5 років (20-25), то будемо вважати, що ширина першого інтервалу буде також 5 років (15-20), відповідно його середина – 17,5. Середнє значення віку визначимо за формулою середньої арифметичної зваженої:
Серед студентів найбільш вагомою віковою групою є 20-25 років, представників цієї групи 10 осіб. Отже, модальний інтервал визначено. За формулою розрахуємо значення моди в межах цього інтервалу: Mo = Нижня межа визначеного модального інтервалу x0 =20, його ширина h =5, частота модального інтервалу fMo =10, частота передмодального інтервалу fMo-1 =8, частота післямодального інтервалу fMo+1 =4. Таким чином, мода дорівнюватиме: Mo = Отже, в групі найчастіше зустрічаються студенти саме з таким віком. Для визначення медіани спочатку з`ясуємо, якою є половина обсягу сукупності. В нашому випадку Me = Нижня межа медіанного інтервалу x0 =20, його ширина h =5. Частота медіанного інтервалу Me = Отже, половина студентів групи мають вік до 22 років, а інша половина – більше 22 років. Задача 2. Використовуючи дані попередньої задачі, зробимо висновки щодо однорідності досліджуваної сукупності. Розв`язок задачі. Для цього побудуємо табл.3. Таблиця 3. Розрахунок показників варіації віку студентів
Використовуючи визначене в попередній задачі значення
Для висновку щодо однорідності досліджуваної сукупності визначимо квадратичний коефіцієнт варіації: Середнє квадратичне відхилення для згрупованих даних розрахуємо за відповідною формулою: Отже, використовуючи дані табл.3:
Отже, значення віку студентів групи відрізняються від середнього значення ( Квадратичний коефіцієнт варіації становитиме:
|

 )
)
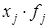
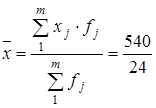 =22,5 (роки).
=22,5 (роки). .
. =
= 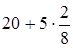 = 21,3 (роки).
= 21,3 (роки). =12. Таким чином, перша кумулятивна частота, що перевищує половину обсягу сукупності, становить
=12. Таким чином, перша кумулятивна частота, що перевищує половину обсягу сукупності, становить 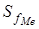 =18. Ця накопичена частота знаходиться в другому інтервалі – 20-25 років. В межах визначеного медіанного інтервалу визначимо значення медіани:
=18. Ця накопичена частота знаходиться в другому інтервалі – 20-25 років. В межах визначеного медіанного інтервалу визначимо значення медіани: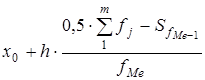 .
.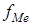 = 10, кумулятивна частота передмедіанного інтервалу
= 10, кумулятивна частота передмедіанного інтервалу 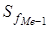 =8. Таким чином,
=8. Таким чином,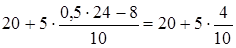 =22 (роки).
=22 (роки).
 р., останню графу таблиці 3 будемо заповнювати таким чином. В першому інтервалі (до 20 років):
р., останню графу таблиці 3 будемо заповнювати таким чином. В першому інтервалі (до 20 років):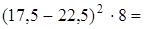 200 і т.д.
200 і т.д.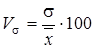 .
.
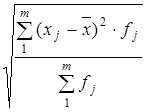 .
. = 4,6 (р.)
= 4,6 (р.) =22,5 р.) в середньому на 4,6 р.
=22,5 р.) в середньому на 4,6 р. =20,4%, що свідчить про однорідність досліджуваної сукупності.
=20,4%, що свідчить про однорідність досліджуваної сукупності.


