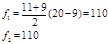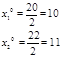Моделирование системы оплаты труда в бригаде из 2-х рабочих(сдельная оплата)Бригада из 2-х рабочих. Имеется плановое задание у 1 и 2 работника П1, П2. Каждая штука продукции дает 1 рубль в фонд оплаты труда, т.о. ФОТ = х1 + х2, х1, х2 - кол-во продукции, которое сделает 1 и 2-й рабочий. Заработок:
Пусть план 1-го рабочего = 9, 2-го – 10. А1 = 20, А2 = 22. Какую стратегию выберет первый рабочий?
Таблица решений:
Псевдо оптимальная точка f2 = (9+10)/2(22-10) = 114 (9;10)- равновесная точка (10;11)- псевдо оптимальная В числителе значение целевой функции для первого, а в знаменателе – для второго. Псевдо оптимальная точка – в этой точке согласуются интересы центра и интересы элементов. Эта точка не является равновесной, т.к. у каждого элемента есть возможность улучшить свои возможности. Первый рабочий решил снизить объем производства: х2 = 11, х1 = 9
Второй, обнаружив, что у него зарплата уменьшилась, тоже уменьшит объем производства. Они вернутся в первый квадрат. Центр, обнаружив такое положение, предлагает перейти на другую систему стимулирования – сдельную. Целевая функция в данном случае: fi = xi (Ai – xi) Оптимальная стратегия:
В случае сдельной оплаты труда работники выберут такую стратегию:
Такое положение является и оптимальным и равновесным.
|
. Уравнительная оплата труда. Вводим А1 и А2 – предельный объем продукции, который может выполнить 1-й и 2-й рабочий. С учетом этого строим функцию (Аi – xi) – функция комфортности труда, т.е. если х = 0, то комфортность = А1. Если рабочий будет работать, то комфортность будет = 0.
- функция удовлетворенности трудом.
105/115,5
