Методы гарантированного результата
Принцип гарантированного результата.
Лицо, принимающее решение не знает значение параметра а, но знает, что: Пример: мы не знаем точную температуру нашего тела, но знаем, в каком диапазоне она находится а могут быть хорошими и плохими Хороший параметр – такой параметр, рост которого способствует улучшению критерия Ф. Плохой параметр – наоборот. Если а хорошее, то его увеличение приводит к росту прибыли. Согласно этому принципу лицо, принимающие решение, исходит из наихудшей гипотезы. Этот подход хорош тем, что хуже, чем предполагается, не будет, а плох тем, что лицо упускает возможные выгоды от лучшего результата. Его используют чаще всего опытные и зрелые люди. Пример: Я возьму с собой зонтик, так как считаю, что при наихудшем варианте может начаться дождь. Также игроки, играющие в преферанс, всегда исходят из того, что в колоде остались худшие карты(7-ки, а не тузы)
В задачах существуют параметры. ЛПР должно обладать информацией о значениях этих параметров. aij – значения этих параметров, cj – коэффициент целевой функции. С точки зрения формализованного описания можем сказать, что ЛПР имеет представление об области допус. значений параметров (а Чем больше ОДЗ, тем больше неопределенность. Решаем задачу «снятия неопределенности». Метод регрессионного прогнозирования. Идея метода заключается в следующем: ЛПР не имеет достоверной информации о значениях параметров на будущие периоды. Однако, он располагает ретро-информацией о значениях этих параметров. Регрессионная модель – описывает изменение состояния объекта во времени. Бывают ситуации, когда изменение параметров характеризуется некоторой тенденцией. Если такое имеет место, то возникает идея построить некоторую функцию, которая описывает эти закономерности а. Есть некоторая статистика. Рассчитывается погрешность: Эти методы применимы только в случаях, когда медленно развиваются процессы. Есть ось времени, необходимо принять упр.решения на несколько будущих периодов. Нам известна ретро-информация об этом параметре(за предыдущие периоды). а = b0 + b1*t b0- начальное состояние параметра b1 – насколько изменяется параметр а при изменении t на единицу Д – дисперсия
Значение а – номинальное значение. Считаем, что а – хороший параметр, то а+Сигма – оптимальный прогноз, а-Сигма – пессимистичный прогноз. (+Сигма;-Сигма) – область допустимых ожидаемых значений Существуют 3 плана: - номинальный - пессимистический - оптимальный
|

 -ОДЗ
-ОДЗ 13. Метод прогнозирования при снятии неопределенности
13. Метод прогнозирования при снятии неопределенности А).
А).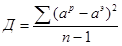 Сигма = Корень из Д
Сигма = Корень из Д


