Seasonal Models. The characteristic equation for matrix D in the (un-normalized) ETS(A,N,A) model is f (λ) = (1 − λ)P(λ) = 0
The characteristic equation for matrix D in the (un-normalized) ETS(A,N,A) model is f (λ) = (1 − λ)P(λ) = 0, where
Thus, D has a unit eigenvalue regardless of the values of the model parameters, and so the model is always unstable.
156 10 Some Properties of Linear Models Similarly, the characteristic equation of D for model ETS(A,Ad,A) is f(λ) = (1 − λ)P(λ) = 0, where P(λ) = λm+1 + (α + β − φ)λm + (α + β − αφ)λm−1 + · · · + (α + β − αφ)λ2 + (α + β − αφ + γ − 1)λ + φ(1 − α − γ). (10.5)
The same argument applies to all of the seasonal models. Thus, the ETS(A,N,A), ETS(A,A,A) and ETS(A,Ad,A) models are forecastable if and only if the roots of P(λ) lie inside the unit circle. Hyndman et al. (2008) use this result to derive the specific conditions for forecastability; these conditions are summarized in Table 10.2. The inequalities involving only α and γ provide necessary conditions To visualize these regions, we have plotted them in Figs. 10.2-10.4. The light-shaded regions represent the forecastability regions; the dark-shaded regions are the usual regions given by 0 < α < 1, 0<β<α, 0 < γ < 1− α, and 0 < φ < 1. The forecastable region for α and γ is illustrated in Fig. 10.2. For large The right hand column of Fig. 10.2 shows that the usual parameter
10.2 Stability and the Parameter Space 157 Table 10.2. Forecastability conditions for models ETS(A,N,A) and ETS(A,Ad,A).
Therefore ETS(A,N,A) models obtained using the usual constraints are always forecastable. The forecastable region for α and β is depicted in Figs. 10.3 and 10.4 for Consequently, we recommend that the usual parameter regions not be
158 10 Some Properties of Linear Models
Fig. 10.2. Light-shaded region: the forecastable region of α and γ for model ETS(A,Ad,A). Dark-shaded region: the usual region where 0 < α < 1 and 0 < γ < 1− α. The right column shows the regions for model ETS(A,A,A) (when φ = 1). These are also the regions for model ETS(A,N,A) as they are independent of β.
|

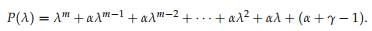 (10.4)
(10.4)









