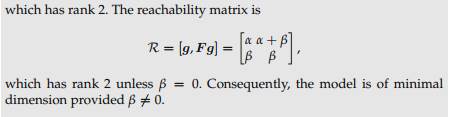Minimal Dimensionality for Linear Models

 

The linear innovations state space models (defined in Chap. 3) are of the form

 

 

The model is not unique; for example, an equivalent model can be obtained
simply by adding an extra row to the state vector and adding a row contain-
ing only zeros to each of w, F and g. Therefore it is of interest to know when
the model has the shortest possible state vector x_t, in which case we say it
has “minimal dimension.”

In particular, we wish to know whether the specific cases of the model
given in Table 2.2 on page 21 are of minimal dimension. The coefficient matri-
ces F, g and w can easily be determined from Table 2.2, and are given below.

 

 

150 10 Some Properties of Linear Models

Here I_k denotes the k × k identity matrix and 0_k denotes a zero vector of
length k.

 

 

 

The matrices for ETS(A,A,N) and ETS(A,A,A) are the same as for
ETS(A,A_d,N) and ETS(A,A_d,A) respectively, but with φ = 1.
The following definitions are given by Hannan and Deistler (1988, pp. 44-45):

Definition 10.1. The model (10.1) is said to be observable if Rank(O) = p where
O=[w,F^′w,(F^′)²w,...,(F^′)^p−1w]

and p is the length of the state vector x_t.

Definition 10.2. The model (10.1) is said to be reachable if Rank(R) = p where
R=[g,Fg,F²g,...,F^p−1g]

and p is the length of the state vector x_t.

Reachability and observability are desirable properties of a state space
model because of the following result from Hannan and Deistler (1988, p. 48):

Theorem 10.1. The state space model (10.1) is of minimal dimension if and only if it is observable and reachable.

 

 

10.1 Minimal Dimensionality for Linear Models 151

 

 

A similar argument can be used (see Exercise 10.1a) to show that the non-seasonal models ETS(A,N,N) and ETS(A,A_d,N) are both reachable and observable, and therefore of minimal dimension.