Seasonal Models
Consider the ETS(A,N,A) model, for which the rank of O < p and the rank of R < p. This is because, for the ETS(A,N,A) model, (F′)p−1 = Fp−1 = Ip. Therefore, model ETS(A,N,A) is neither reachable nor observable. A similar argument (Exercise 10.1b) shows that models ETS(A,A,A) and ETS(A,Ad,A) are also neither reachable nor observable. These problems arise because of a redundancy in the model. For example, the ETS(A,N,A) model is given by yt = ℓt−1 + st−m + εt, where the level and seasonal components are given by
So both the level and seasonal components have long run features due to unit roots. In other words, both can model the level of the series, and the seasonal component is not constrained to lie anywhere near zero. This is the same problem that led to the use of normalizing in Chap. 8. Let L denote the lag operator defined by Lyt = yt−1. Then, by expanding
S(L) = 1 + L + ··· + Lm−1 represents the seasonal summation operator and θ(L) = m−1 [(m − 1) + (m − 2)L + · · · + 2Lm−3 + Lm−2]. The long run component ℓ∗t shouldbepartofthelevelterm. This leads to an alternative model specification where the seasonal equa-
152 10 Some Properties of Linear Models The other equations remain the same, as the additional level term can be
In other words, the seasonal term is calculated as in the original models, but is then adjusted by subtracting the average of the last m shocks. The effect of this adjustment is equivalent to the normalization procedure outlined in Chap. 8, in which the seasonal terms st,..., st−m+1 are adjusted every time period to ensure that they sum to zero. Models using the seasonal component (10.2) will be referred to as “normalized” versions of ETS(A,N,A), ETS(A,A,A) and ETS(A,Ad,A). It can be shown (Exercise 10.1c) that the normalized models are of minimal dimension.
|

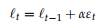
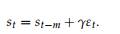 and
and
 (10.2)
(10.2)
 Noting that θ(L)/S(L) = [1 −1mS(L)]/(1−Lm), we see that(10.2) can be
Noting that θ(L)/S(L) = [1 −1mS(L)]/(1−Lm), we see that(10.2) can be 


