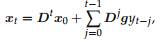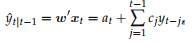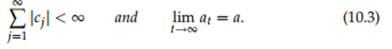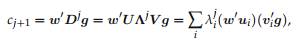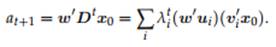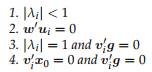Stability and the Parameter Space

In Chap.3, we found (p. 36) that, for linear models of the form (10.1), we could write the state vector as

 

where D = F − gw^′ is the discount matrix. So for initial conditions to have a negligible effect on future states, we need D^t to converge to zero. There-
fore, we require D to have all eigenvalues inside the unit circle. We call this condition stability (following Hannan and Deistler 1988, p. 48).

Definition 10.3. The model (10.1) is said to be stable if all eigenvalues of D =

F − gw^′ lie inside the unit circle.

Stability is a desirable property of a time series model because we want models where the distant past has a negligible effect on the present state.
In Chap. 3, we also found that

 

where a_t = w^′ D^t−1x₀ and c_j = w^′ D^j−1g. Thus, the forecast is a linear func-
tion of the past observations and the seed state vector. This result shows that
for a model to be stable, we require the weaker forecastability condition:

Definition 10.4. The model (10.1) is forecastable if

 

Obviously, any model that is stable is also forecastable.

 

 

10.2 Stability and the Parameter Space 153

On the other hand, it is possible for a model to have a unit eigenvalue for D, but to satisfy the forecastability condition (10.3). In other words, an unstable model can still produce stable forecasts provided the eigenvalues which cause the instability have no effect on the forecasts. This arises because D may have unit eigenvalues where w^′ is orthogonal to the eigenvectors corresponding to the unit eigenvalues.

To avoid complications, we will assume that all the eigenvalues are dis-
tinct. In this case, we can write the eigendecomposition of D as D = U ΛV, where the columns of U are the eigenvectors of D, Λ is a diagonal matrix containing the eigenvalues of D, and V = U⁻¹. Then

 

where u_i is a column of U (a right eigenvector) and v_i is a row of V (a left eigenvector). By inspection, we see that the sequence converges to zero pro-
vided either |λ_i | < 1, w^′u_i = 0 or v^′ig^{=0,foreachi.Further,thesequence} only converges under these conditions. Similarly,

 

 

In this case, the sequence converges to a constant if and only if either |λ_i | ≤
1, w^′u_i = 0 or v_ix₀ = 0, for each i. Thus, we can restate forecastability as
follows.

Theorem 10.2. Let λ_i denote an eigenvalue of D = F − gw^′, and let u_i be the
corresponding right eigenvector and v_i the corresponding left eigenvector. Then the
model (10.1) is forecastable if and only if, for each i, at least one of the following four
conditions is met:

 

The concept of forecastability was noted by Sweet (1985) and Lawton
(1998) for ETS(A,A,A) (additive Holt-Winters) forecasts, although neither
author used a stochastic model as we do here. The phenomenon was also
observed by Snyder and Forbes (2003) in connection with the ETS(A,A,A)
model. The first general definition of this property was given by Hyndman
et al. (2008).

We now establish stability and forecastability conditions for each of the linear models. For the damped models, we assume that φ is a fixed damp-
ing parameter between 0 and 1, and we consider the values of the other parameters that would lead to a stable model.

 

 

154 10 Some Properties of Linear Models

 

Again, for ETS(A,A,N) and ETS(A,A,A), the corresponding result is obtained from ETS(A,A_d,N) and ETS(A,A_d,A) by setting φ = 1.

 

The stability conditions for models without seasonality (i.e., ETS(A,N,N),
ETS(A,A,N)and ETS(A,A_d,N)) are summarized in Table 10.1. These are given

 

 

10.2 Stability and the Parameter Space 155

 

Fig. 10.1. Parameter spaces for model ETS(A,A_d,N). The right hand graph shows the
region for model ETS(A,A,N) (when φ = 1). In each case, the light-shaded regions rep-
resent the stability regions; the dark-shaded regions are the usual regions constructed
by restricting each parameter in the conventional parameterization to lie between 0
and 1.

 

in McClain and Thomas (1973) for the ETS(A,A,N) model; results for the
ETS(A,A_d,N) and ETS(A,N,N) models are obtained in a similar way. To
visualize these regions, we have plotted them in Fig. 10.1. The light-shaded
regions represent the stability regions; the dark-shaded regions are the usual
regions defined by 0 < β < α < 1. Note that the usual parameter region
is entirely within the stability region in each case. Therefore non-seasonal
models obtained using the usual constraints are always stable (and always
forecastable).