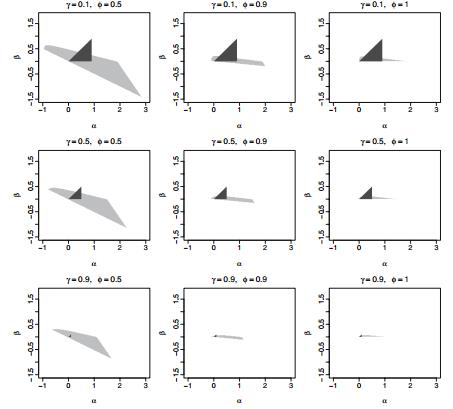
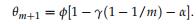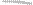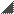Parameter regions for monthly data
Fig. 10.4. Light-shaded region: the forecastable region of α and β for model
and
Note that this is equivalent to (10.5) if we reparameterize the model,
10.4 Exercises 161 the standard ETS(A,Ad,A) model are the same as the stability conditions for the normalized ETS(A,Ad,A) model, apart from this minor reparam-
10.3 Conclusions With the non-seasonal exponential smoothing models, our results are clear: the models are of minimal dimension and are stable using the usual con- With the seasonal exponential smoothing methods, the situation is more The normalized model circumvents this problem by requiring the seasonal
10.4 Exercises
Exercise 10.1. a. Show that the non-seasonal models ETS(A,N,N) and ETS(A,Ad,N) are of b. Show that the seasonal models ETS(A,A,A) and ETS(A,Ad,A) are not of c. Show that the normalized seasonal models ETS(A,N,A), ETS(A,A,A) and ETS(A,Ad,A) are of minimal dimension. d. Show that the (unnormalized) seasonal models ETS(A,A,A) and ETS(A,Ad,A) are of minimal dimension if the level component is omitted from the models. (This is an alternative to normalization). Exercise 10.2. Complete Example 10.3 by showing that u is proportional to [−1, 0, 1,..., 1] for the ETS(A,A,A) model. Exercise 10.3. The expression xt = Dxt−1 + gyt also applies to some of the nonlinear models discussed in Chap. 4. Use this observation to write down the stability conditions for the relevant nonlinear models.
|

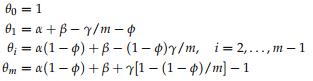 where
where