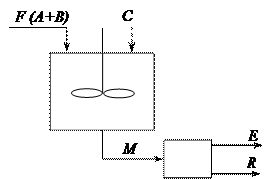
Одноступенчатая экстракция
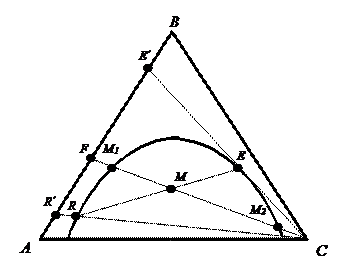
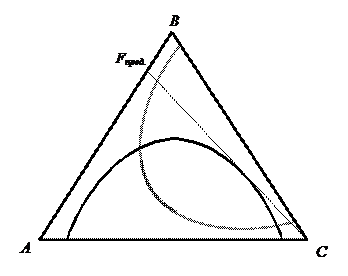
Для определения min расхода растворителя проводим прямую через точки F и С и находим точку М 1 на пересечении этой линии с равновесной. По правилу рычага Минимальный расход растворителя
где F – расход сырья. Максимальный расход растворителя
Действительный расход растворителя
где
Проведя ноду через точку М, на ее концах находим точки Е и R, которые характеризуют составы равновесных рафинатного и экстрактного растворов. Количество полученных растворов находим по правилу рычага:
Проводим прямую через точки R и С и на стороне АВ находим точку R´; которая характеризует состав рафината. Количество полученного рафината:
Аналогично находим состав экстракта, проводим прямую через С и Е и находим Е´;.
на отрезке Fпред В, то при смешении с растворителем расслаивания не произойдет. Для решения этой задачи можно подобрать другой растворитель, в котором лучше будет растворяться компонент А. Можно изменить положение бинодальной кривой, изменяя температуру экстракции. Вывод: при одноступенчатой экстракции происходит грубое разделение с большими затратами. Для снижения затрат и повышения качества очищаемого продукта используют многоступенчатую экстракцию.
|
.
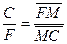
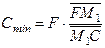
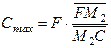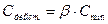
- коэффициент избытка растворителя
< 
< 
.
;
.
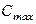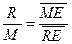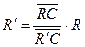
другой растворитель.
