Лабораторна робота № 5. Мета роботи — оволодіння прийомом програмування для знаходження найбільшого та найменшого значення функції з використанням оператора-функції
Знаходження найбільшого та найменшого значення функції
Мета роботи — оволодіння прийомом програмування для знаходження найбільшого та найменшого значення функції з використанням оператора-функції.
Теоретична частина
Змінні величини та функції, що їх визначають Інтервалом від a до b називається сукупність усіх чисел х, що задовольняють одну з наступних подвійних нерівностей:
Закритий інтервал називається відрізком і позначається [а, b]; відкритий інтервал позначається (а, b); напіввідкриті інтервали позначаються відповідно [а, b) та (a, b]. Змінною називається величина, що приймає різні числові значення. Областю визначення змінної називається сукупність усіх числових значень, які вона приймає. Вона може складатися з одного чи кількох інтервалів та з окремих точок. Взаємопов’язана зміна змінних називається функціональною залежністю. При вивченні функціональної залежності між двома змінними вважають, що одна з них є незалежною змінною, якій можна надавати довільні значення з області її визначення, а друга – залежною від неї. Незалежна змінна називається аргументом, а залежна – функцією. Н. І. Лобачевському належить наступне визначення поняття функції: Змінна у називається функцією змінної x, якщо кожному значенню х, відповідає певне значення у. Для скорочення запису застосовується символічне позначення функцій: у= f(x), S= j (t), u= F (u),… Якщо функція від х позначена символом Р(х), то Р (а) позначає конкретне значення цієї функції при х=а. Так, якщо Р (х)= x2+ 2х- 5, то Р (3)= 32+2*3- 5= 10; Р (0)= -5; Р(а)= а2+ 2а-5. Основними елементарними функціями називаються: 1) степенева функція у=хn; 2) показникова функція y=ax, a>0; 3) логарифмічна функція y= loga x, a>0; 4) тригонометричні функції y= sin x, y= cos x, y=tg x, y=ctg x, y=sec x, y=cosec x; 5) обернені триногометричні функції y=arcsin x, y =arccos x, y=arctg x, y= arcctg x. Функції, що задані однією формулою за допомогою скінченого числа арифметичних дій та операцій, називаються елементарними. Наприклад:
Всі інші функції називаються неелементарними. Наприклад, неелементарною є функція, що визначається кількома різними формулами для різних інтервалів зміни аргументу:
Функція f(x), що має властивість f(x) = f(-x), називається парною, наприклад х2, cos x, а та, що має властивість f(x)=-f(-x), непарною,наприклад x3, sin x. Багато функцій є ні парними, ні непарними, наприклад, ax,
Область визначення (існування) функції Областю визначення функції називається сукупність усіх точок числової осі, в яких вона має певні дійсні значення. Для багатьох функцій областю визначення буде не вся числова вісь, а тільки її частина. Так, для функції Основні елементарні функції мають наступні області визначення:
При знаходженні області визначення елементарної функції, заданої формулою Y=f(x), треба звертати увагу на такі елементи формули:
Максимум та мінімум (екстремум) функції Значення функції f(x) в точці х0 називається максимумом (мінімумом), якщо воно є найбільшим (найменшим) у порівнянні з її значеннями в усіх достатньо близьких точках зліва та справа від х0. Функція може мати екстремум (максимум чи мінімум) тільки в тих точках, які лежать в області визначення функції і де її похідна дорівнює нулю або не існує. Такі точки називаються критичними. У відповідних точках графіка функції дотична паралельна до осі Ох (у¢ = 0), або осі ординат (у¢ = ¥). На графіку функції (рис. 5.1) добре видно, що точками екстремуму є всі точки, де функція змінює свою поведінку та неперервна. Точки х1 и х4, при переході через які аргумента х зростання функції змінюється на спадання, є точками максимуму, а точки х3 и х6, при переході через які аргумента х спадання змінюється на зростання, є точками мінімуму. Так як поведінка функції характеризується знаком її похідної, то функція буде мати екстремум в тих точках, де її похідна змінює знак, а сама функція неперервна. Звідси витікає наступне правило дослідження функції на екстремум Щоб знайти точки екстремуму функції у=f(x),в яких вона неперервна, треба: І. Знайти похідну у ' та критичні точки, в яких у=0 або не існує, а сама функція неперервна, і які лежать в області визначення функції. ІІа. Визначити знак у ' зліва та справа від кожної критичної точки.
Якщо при переході аргументу х через критичну точку х0: · у ' змінює знак з + на –, то х0 є точкою максимуму; · у ' змінює знак з – на +, то х0 є точкою мінімуму; · y ' не змінює знака, то в точці х0 нема екстремуму. Іноді легше досліджувати критичні точки, де у ' =0, по знаку другої похідної, — замість правила IIа можна використовувати наступне правило: IIб. Знайти другу похідну у '' і визначити її знак в кожній критичній точці. Якщо в критичній точці х0, де у=0 · у'' > 0, то х0 -- точка мінімуму; · у'' < 0, то х0 – точка максимуму; · у'' = 0, то питання про наявність екстремуму в точці х0 залишається відкритим. Таку критичну точку, як і будь-яку іншу, можна досліджувати по правилу IIa. Далі треба знайти екстремуми функції, тобто обчислити значення функції в знайдених точках екстремуму. При дослідженні на екстремум деяких типів функцій можливі значні спрощення. Наприклад, якщо функція являє собою дріб з постійним чисельником або корінь з цілим додатнім показником.
Найбільше та найменше значення функції Найбільшим значенням функції називається саме більше, а найменшим значенням – саме менше з усіх її значень.
Знаходження найбільшого і найменшого значення неперервних функцій базується на наступних властивостях цих функцій:
Звідси витікає практичне правило для знаходження найбільшого або найменшого значення функції f(x) на відрізку [a,b], де вона неперервна:
Оператор-функція Оператор-функцію застосовують, коли необхідно багаторазово обчислювати функцію при різних значеннях аргументу, як, наприклад, при наближеному розв’язанні алгебраїчних та трансцендентних рівнянь різними методами. Вона дає змогу користувачеві самостійно задавати вид досліджуваної функції. Але використання цього оператору має свої особливості: 1. Оператор-функція DEF FN повинен бути розміщений до тих операторів програми, в яких є звернення до оператору-функції; 2. Оператор-функцію не можна розміщувати в області циклу FOR...NEXT. Функція DEF FN може бути записана в блочній або в лінійній формі. Лінійна форма DEF FN і м’я[(параметри)]=вираз
|

 ;
; 

 .
. областю визначення є напіввідкритий інтервал
областю визначення є напіввідкритий інтервал 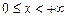 ; для функції
; для функції 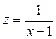 область визначення складається з двох інтервалів:
область визначення складається з двох інтервалів: 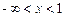 та
та 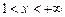 .
.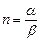 при непарному
при непарному 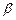 визначена на всій числовій осі
визначена на всій числовій осі 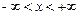 , а при парному
, а при парному 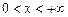
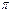 ¤ 2, k=0, +1, +2, …;
¤ 2, k=0, +1, +2, …; 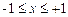 ;
;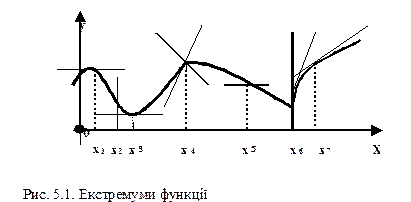

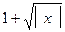 має найменше значення, рівне одиниці, але не має найбільшого значення (рис. 5.2).
має найменше значення, рівне одиниці, але не має найбільшого значення (рис. 5.2).



