Лабораторна робота № 12
Взаємозв’язок індексів у квадратній матриці.
Мета роботи – оволодіння навичками обробки елементів, які розташовані на діагоналях та паралелях до діагоналей квадратної матриці.
Теоретична частина
По аналогії з геометрією, де квадрат має діагоналі, такі ж діагоналі можна умовно проставити в квадратний матриці. Так в квадратній матриці А(N,N) (рис.12. 1) проведено діагоналі, які називаються головною і бічною.
Умова належності елементів до головної діагоналі: i=j або i–j=0 (нижче головної діагоналі i > j; вище головної діагоналі i < j). Умова належності елементів бічної діагоналі: i + j = N +1 (нижче бічної діагоналі i+j > N+1; вище бічної діагоналі i+j < N+1). В квадратній матриці можна умовно провести паралелі до головної діагоналі (рис. 12. 2) і до бічної діагоналі (рис. 12. 3):
Елементи, які розташовані на паралелі до головної діагоналі: 1 паралель - A1,4 (i – j = -3); 2 паралель - A1,3; A2,4 (i – j = -2); 3 паралель - A1,2; A2,3; A3,4 (i – j = -1); Головна діагональ A1,1; A2,2; A3,3; A4,4 (i – j = 0); 4 паралель - A2,1; A3,2; A4,3 (i – j = 1); 5 паралель - A3,1; A4,2 (i – j = 2); 6 паралель - A4,1 (i – j = 3);
Розглянемо матрицю А(N, N). Неважко побачити, що елементи головної діагоналі мають незмінну різницю індексів. Таку ж властивість мають елементи, які розташовані на паралелях до головної діагоналі (відрізняється тільки значення константи). Знаючи значення константи i – j = z, де z – це число, яке характеризує паралель, можна вибрати елементи діагоналі або будь-якої паралелі. Звичайно перегляд матриці ми реалізовували подвійним циклом. Якщо потрібно вибрати елементи, що належать до кожної з паралелей, то організується ще один зовнішній цикл. Всі паралелі переглядаються зовнішнім циклом:
· паралелі нижче головної діагоналі переглядаються циклом: FOR Z = 1 TO N – 1. Аналогічна ситуація має місце з бічною діагоналлю.
Елементи, які розташовані на паралелі до бічної діагоналі: 1 паралель - A1,1 (i + j = 2); 2 паралель - A2,1; A1,2 (i + j = 3); 3 паралель - A3,1; A2,2; A1,3 (i + j = 4); Бічна діагональ - A4,1; A3,2; A2,3; A1,4 (i + j = 5); 4 паралель - A4,2;A3,3; A2,4 (i + j = 6); 5 паралель - A4,3; A3,4 (i + j = 7); 6 паралель - A4,4 (i + j = 8);
Елементи бічної діагоналі та паралелі до неї мають незмінну суму індексів, тобто i + j = z,де z – це число, яке характеризує паралель. Якщо треба переглянути елементи в квадратній матриці A(N, N) і вибрати ті з них, які знаходяться:
FOR Z = N + 2 TO 2* N. Застосування цих викладок зрозуміло з наступного прикладу. Приклад 1. Знайти суму елементів кожної паралелі до головної діагоналі, розташованої нижче головної діагоналі.
'Приклад1 INPUT "Введіть розмірність матриці - N"; N DIM A(N, N) PRINT "Введіть масив"; FOR I = 1 TO N FOR J = 1 TO N INPUT A(I, J) NEXT J,I CLS PRINT "Початковий масив"; FOR I = 1 TO N FOR J = 1 TO N PRINT A(I, J); NEXT J NEXT I FOR Z = 1 TO N - 1 S = 0 FOR I = 1 TO N FOR J = 1 TO N IF I - J = Z THEN S = S + A(I, J) END IF NEXT J NEXT I PRINT "СУМА="; S NEXT Z END
Приклад 2. Задана матриця X(Y,Y). Створити нову квадратну матрицю, усунувши з початкової головну діагональ і останній стовпчик. Надрукувати трикутник елементів нової матриці, які розташовані нижче бічної діагоналі, і знайти добуток елементів цього трикутника.
REM Приклад2. Зменшення розміру матриці INPUT "Введіть розмірність матриці - Y";Y DIM X(Y,Y), C(Y-1,Y-1) PRINT "Введіть масив"; FOR I = 1 TO Y FOR J = 1 TO Y INPUT X(I, J) NEXT J,I CLS REM C(Y-1,Y-1) – нова матриця FOR I=1 TO Y-1 FOR J=1 TO Y-1 IF I>=J THEN С(I,J)=X(I+1,J) ELSE C(I,J)=X(I,J) NEXT J,I ‘ Друк трикутника ‘ Обчислення добутку P=1 FOR I=2 TO Y-1 PRINT TAB(70-I) FOR J=Y-I+2 TO Y-1 ‘ Під бічною діагоналлю PRINT C(I,J); P=P*C(I,J) NEXT J NEXT I PRINT "Добуток= "; P END
Приклад 3. Дано масив C(M,M). Створити одновимірний масив з добутків тієї частини кожного стовпчика, яка знаходиться нижче головної діагоналі. Розв’язання. Позначимо Y — створюваний одновимірний масив, L — його індекс. Шуканий масив буде мати розмір M-1, тому, що в останньому (M-тому) стовпчику під діагоналлю елементів немає. Умова розміщення елементів квадратної матриці нижче головної діагоналі: I>J
REM Задача REM Ввід вхідних даних. I NPUT M: DIM C(M,M),Y(M-1) FOR I=1 TO M: FOR J=1 TO M INPUT C(I,J) NEXT J,I ‘Формування та друк масива Y L=0 FOR J=1 TO M-1 P=1 FOR I=1 TO M IF I>J THEN P=P+C(I,J) NEXT I L=L+1: Y(L)=P: PRINT Y(L) NEXT J END
Зразок виконання завдання
Завдання. Дано масив C(N, N). Знайти мінімальний елемент серед елементів, розташованих під бічною діагоналлю. З елементів, розташованих на паралелі, розташованій безпосередньо під головною діагоналлю, створити одновимірний масив D. Програма подана нижче, а відповідна блок-схема зображена на рис. 12.4
CLS 'Лабораторна робота № 12. Робота з двовимірними масивами INPUT "Введіть розмір масиву -N";N DIM C(N, N), D(N - 1) MIN = 1E+20 K = 0 FOR I = 1 TO N: FOR J = 1 TO N: I NPUT C(I, J): NEXT J, I CLS PRINT "Вхідний масив"; FOR I = 1 TO N: FOR J = 1 TO N: PRINT C(I, J): NEXT J, I PRINT "Зформований масив"; FOR I = 1 TO N FOR J = 1 TO N ' Знаходження мінімального елементу серед елементів, ' розташованих під бічною діагоналлю, IF I+J > N+1 AND C(I,J) < MIN THEN MIN = C(I,J) ' Створення одновимірного масиву D(K) з елементів, ' Розташованих на паралелі під головною діагоналлю IF I - J = 1 THEN K = K + 1 D(K) = C(I, J) PRINT D(K); END IF NEXT J NEXT I PRINT "Мінімальний елемент -"; MIN END
1. Де розташована головна діагональ в квадратній матриці? 2. Де розташована бічна діагональ в квадратній матриці? 3. Умова належності елемента до головної діагоналі? Нижче діагоналі? Вище діагоналі? 4. Умова належності елемента до бічної діагоналі? Нижче діагоналі? Вище діагоналі? 5. Як переглянути елементи окремої паралелі до діагоналі?
Варіанти завдань.
1. Скласти алгоритм і програму обчислення суми квадратів елементів окремо головної і бічної діагоналей матриці А(5,5). Елементи матриці А задати самостійно. Надрукувати матрицю А та знайдені суми квадратів. 2. Задано масив Р(4,4), в якому відсутні нульові елементи. Отримати новий масив діленням всіх елементів вхідного масиву на найменший елемент масиву. Визначити суму елементів головної діагоналі отриманого масиву. Результати надрукувати. Елементи масиву Р задати самостійно. 3. В масиві В (Х, Х) визначити добуток елементів, розташованих одночасно під головною діагоналлю та лівіше четвертого стовпчика. 4. Дано масив A (N, N). Сформувати масив S із сум тих елементів рядків, які розташовані вище бічної діагоналі, та масив P із добутків елементів на паралелях, що лежать нижче бічної діагоналі. Одержані масиви об’єднати в масив С наступним чином: C (S1, P1, S2, P2, S3, P3,…). 5. В масиві А (Х, Х) знайти добутки елементів кожної паралелі до бічної діагоналі та самої діагоналі, і знайдені добутки об’єднати в одновимірний масив. 6. Знайти суму елементів головної діагоналі, збільшену на значення максимального елемента в масиві В (M, M). 7. В квадратній матриці знайти добуток квадратів елементів бічної діагоналі. 8. В квадратній матриці знайти добуток елементів, розташованих вище бічної діагоналі. 9. Дано масив C (V,V). Знайти максимальний елемент з елементів, розташованих над головною діагоналлю та під другим рядком. 10. Знайти мінімальний елемент під бічною діагоналлю та під другим рядком квадратної матриці. 11. Знайти добуток від¢ємних елементів бічної діагоналі та їх кількість в масиві А (М, М). 12. Знайти добуток додатних елементів під бічною діагоналлю в квадратній матриці. 13. Знайти середнє арифметичне елементів бічної діагоналі та середнє арифметичне головної діагоналі в квадратній матриці. 14. Знайти максимальний та мінімальний елементи над головною діагоналлю в масиві С (М, М). 15. Дано масив А(М,М) знайти: 1) Суми елементів, розташованих на кожній паралелі до головної діагоналі та на самій діагоналі. Об’єднати їх в масив. 2) Добутки елементів, розташованих на кожній паралелі до головної діагоналі та на самій діагоналі. Об’єднати їх в масив. 3) Кількості елементів, розташованих на кожній паралелі до головної діагоналі та на самій діагоналі. Об’єднати їх в масив. Елементи А(1,М) та А(М,1) виключити з розгляду. 4) Середні арифметичні значення елементів, розташованих на кожній паралелі до головної діагоналі та на самій діагоналі. Об’єднати їх в масив. Елементи А(1,М) та А(М,1) виключити з розгляду. 5) Суми додатних елементів, розташованих на кожній паралелі до бічної діагоналі і на самій діагоналі. Об’єднати їх в масив. Елементи А(1,1) та А(М,М) виключити з розгляду. 6) Добутки елементів, розташованих на кожній паралелі до бічної діагоналі та на самій діагоналі. Об’єднати їх в масив. 7) Кількості нульових елементів, розташованих на кожній паралелі до бічної діагоналі та на самій діагоналі. Об’єднати їх в масив. Елементи А(1,1) та А(М,М) виключити з розгляду. 8) Середні арифметичні значення елементів, розташованих на кожній паралелі до бічної діагоналі та на самій діагоналі. Об’єднати їх в масив. Елементи А(1,М) и А(М,1) виключити з розгляду. 16. Дано масив А(N,N). Сформувати масив S із сум тих елементів рядків, які розміщені вище головної діагоналі, та масив P з добутків елементів на паралелях, які лежать нижче головної діагоналі. Отримані масиви об’єднати в масив С наступним чином: C (S1,S2, S3,...,P1,P2,P3,...) 17. Дано масив B(X,X). Сформувати масив S із сум тих елементів стовпчиків, які розміщені над бічною діагоналлю, та масив Р з добутків елементів на паралелях, які лежать під бічною діагоналлю. Отримані масиви об’єднати в масив С наступним чином: C (S1,P1, S2,P2, S3 ,P3,...). 18. Дано масив B(M,M). Сформувати масив S із сум тих елементів стовпчиків, які розміщені під головною діагоналлю, масив Р з добутків елементів на паралелях, які лежать над головною діагоналлю. Отримані масиви об’єднати в масив С наступним чином: C (S1,S2, S3,...,P3,P2,P1). 19. Дано масив А(X,X). Сформувати масив S із сум тих елементів рядків, які розміщені під головною діагоналлю, та масив Р з добутків елементів на паралелях, які лежать над головною діагоналлю. Отримані масиви об’єднати в масив С наступним чином: C (S1,P1, S2,P2, S3 ,P3,...).
|


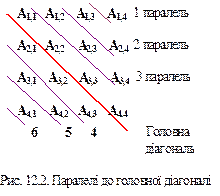

 Програма
Програма Контрольні запитання
Контрольні запитання


