Лабораторна робота № 10

Двовимірні масиви.

Знаходження кількісних характеристик матриці

Мета роботи – оволодіння навичками вводу та виводу двовимірних масивів, знаходження їх кількісних характеристик та перетворення одновимірних масивів в двовимірні і навпаки.

Теоретична частина

 

В багатьох випадках інформація може бути представлена більш компактно, чітко та зрозуміло, якщо для її представлення використовується більше, ніж один просторивий вимір.

QBASIC надає можливість використовувати масиви від одного до восьми вимірів, хоч розмірність більше трьох неможливо представити графічно.

Двовимірні масиви даних найбільш просто представити у вигляді таблиці (матриці). Наприклад, таблиця множення може бути записана в масиві TABL %(9,9):

Двовимірний масив, як і одновимірний, оголошується оператором DIM в формі:

DIM Назва масива(індекс_1, індекс_2),

де індекс_1 характеризує перший вимір (рядок), а індекс_2 характеризує другий вимір (стовпчик), при чому

індекс_1 = максимальному значенню індекса1 по першому виміру,

індекс_2 = максимальному значенню індекса2 по другому виміру.

QBASIC додатково до цих можливостей дозволяє задавати границі значень індекса у вигляді

[ нижнє_значення TO верхнє значення ].

Наприклад, оператор DIM A%(5,6) описує цілочислений двовимірний масив A% розміром 6x7, тобто 6 рядків (з 0-го по 5-ий) та 7 стовпчиків (з 0-го по 6-й); а оператор DIM A% (1 ТО 5, 1 ТО 6) описує цілочислений двовимірний масив A% розміром 5x6. Дія оператора DIM у випадку двовимірного масиву аналогічні до одновимірного масиву.

Наступна програма демонструє як можна зберегти таблицю множення у масиві з ім’ям TABL %.

 

‘ Таблиця множення

DEFINT A-Z

DIM TABL % (1 TO 9, 1 TO 9)

TAB (7);

REM Перший цикл друкує номер стовпчика

FOR NCOL=1 TO 9: PRINT NCOL;: NEXT NCOL

PRINT

REM Другий цикл обчислює та друкує результати

FOR NSTR=1 TO 9

PRINT NSTR; TAB (7);

FOR NCOL=1 TO 9

TABL (NSTR, NCOL)=NSTR*NCOL

PRINT TABL (NSTR, NCOL);

NEXT NCOL

PRINT

NEXT NSTR

END

 

При вивченні вкладенних циклів згадувалось, що вони часто використовуються разом з масивом. Запропонована програма є прикладом такого випадку: зовнішній цикл змінює другий індекс, внутрішній змінює перший індекс масиву. Таким чином, масив TABL% заповнюється рядок за рядком:

TABL%(1,1), TABL%(1,2),..., TABL%(1,9),

TABL%(2,1), TABL%(2,2),..., TABL%(2,9),

TABL%(3,1),...

Часто при розв`язанні задач потрібно оперувати даними, що представлені у табличній формі, тобто з’являється необхідність оголосити двовимірний масив та ввести його дані з клавіатури. Для організації вводу пропонується наступна програма, яка виводить масив у вигляді таблиці.

 

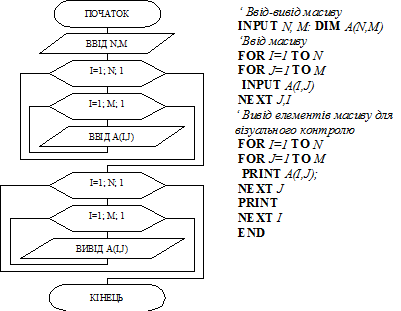
Приклад 1. Нехай треба ввести з клавіатури масив A (N,M).

Перша частина програми забезпечує ввід елементів порядково. Зовнішній цикл змінює індекс рядка, внутрішній змінює індекс стовпчика.

A(1,1), A(1,2),..., A(1,M),

A(2,1), A(2,2),..., A(2,M),

A(3,1), A(3,2),..., A(3,M),

...

 

Приклад 2. Задано двовимірний масив BA (10,20). Знайти середнє арифметичне його додатних елементів.

 

Приклад 3. Задано двовимірний масив A(K,L). Знайти добуток його елементів.

REM Добуток всіх елементів масиву

INPUT K,L: DIM A(K,L)

‘ Ввід елементів масиву

FOR I=1 TO K: FOR J=1 TO L: INPUT A(I,J): NEXT J,I

‘ Вивід елементів масиву для візуального контролю

FOR I=1 TO K

FOR J=1 TO L

PRINT A(I,J);

NEXT J

PRINT

NEXT I

P=1

FOR I=1 TO K: FOR J=1 TO L: P=P*A(I,J): NEXT J,I

PRINT P

END

Якщо хоча б один елемент у масиві A(K,L) дорівнює нулю, то добуток буде дорівнювати нулю. Якщо в добуток повинні входити тільки ненульові елементи, то необхідно враховувати цю умову.

В подальшому домовимося називати двовимірний масив матрицею та не виводити його після початкового вводу на візуальний контроль для економії місця та часу.

Приклад 4. Задана матриця B(N,M), де N>5, M>10. Знайти кількість парних елементів, що розташовані вище 4-го рядка та правіше 5-го стовпчика.

REM Робота з областями матриці

INPUT N,M: DIM В(N,M)

FOR I=1 TO N: FOR J=1 TO M: INPUT B(I,J): NEXT J,I

K=0

FOR I=1 TO 3

FOR J=6 TO M

IF B(I,J)/2=INT(B(I,J)/2) THEN K=K+1

NEXT J,I

PRINT K

END

Перетворення одновимірних масивів у двовимірні та навпаки

 

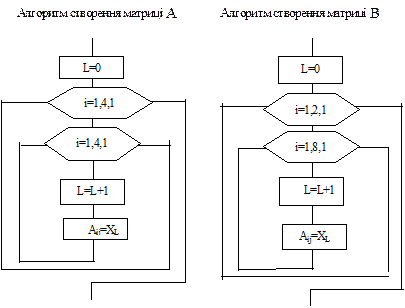
Для формування матриці з елементів одновимірного масиву необхідно, по-перше, знати розміри створюваної матриці, по-друге, кількість елементів вихідного масиву повинна бути достатньою.

Нехай маємо масив X(16). З нього можна створити матриці A(4,4) або B(2,8).

 

 

Очевидно, що протилежне перетворення буде відрізнятися тільки присвоєнням: X_L=Ai,j або X_L=Bi,j.

Розглянемо питання визначення розміру квадратної матриці.

Нехай з елементів вихідного масиву X(93) необхідно створити квадратну матрицю максимально можливого розміру. Простим підбором можна визначити, що розмір найбільшої матриці — 9х9. В загальному випадку розмір найбільшої квадратної матриці визначається як N=[ ], де M — розмір вихідного одномірного масиву. В наведеному прикладі N=[ ]=[9,64]=9.

Приклад 5. Здано масиви A(N), B(M,N). Із додатних елементів заданих масивів створити квадратну матрицю D(X,X), де X >=2. Значення X вибрати таким, щоб масив D мав максимально можливі розміри.

Розв’язання. Алгоритм розіб’ємо на дві частини. Спочатку з додатних елементів заданих масивів сформуємо проміжний одновимірний масив С. Використовуючи проміжний масив, визначимо розміри створюваної квадратної матриці та сформуємо її. Ввід вхідних масивів та формування проміжного масиву виконується в одному циклі; L — індекс масиву С.

 

REM Формування квадратної матриці

REM Ввід вхідних даних та створення проміжного масиву С

INPUT N: DIM A(N),B(M,N),C(N+M*N)

L=0

FOR I=1 TO N

INPUT A(I)

IF A(I)>0 THEN L=L+1: C(L)=A(I)

NEXT I

FOR I=1 TO M: FOR J=1 TO N

INPUT B(I,J)

IF B(I,J)>0 THEN L=L+1: C(L)=B(I,J)

NEXT J: NEXT I

X=INT(SQR(L))

IF X<2 THEN PRINT “Масив створити неможливо”: GOTO 20

K=0: DIM D(X,X)

FOR I=1 TO X: FOR J=1 TO X

K=K+1: D(I,J)=C(K)

PRINT D(I,J);

NEXT J: PRINT: NEXT I

END

 

Приклад 6. Задана матриця B(N,M). Знайти значення максимального елементу матриці. Результат вивести на друк.

 

Контрольні запитання

1. Що таке двовимірний масив? Як він оголошується в програмі?
2. Особливості вводу двовимірних масивів.

3. Особливості вибору максимального та мінімального елементів із двовимірного масиву.

1. Особливості вибору з двовимірного масиву парних(непарних) елементів.
2. Особливості перетворення одновимірних масивів в двовимірні.

Варіанти завдань

 

1. Задана матриця K(N,L). Знайти в ній суму додатних елементів.

2. Задана матриця K(N,L). Знайти суму від’ємних елементів, більших по модулю п’яти.

3. Задана матриця K(N,L). Знайти кількість від’ємних, кратних трьом елементів.

4. Задана матриця K(N,L). Знайти кількість додатних парних елементів.

5. Задана матриця K(N,L). Знайти добуток усіх елементів.

6. Задана матриця K(N,L). Знайти добуток усіх додатних елементів, не більших п’яти.

7. Задано двовимірний масив A(N,M). Знайти середнє арифметичне його парних елементів.

8. Задана матриця K(A,B). Знайти середнє геометричне її додатних елементів.

9. Задана матриця A(N,M). Знайти середнє геометричне парних додатних елементів.

10. Задано двовимірний масив Q(C,S). Знайти середнє геометричне усіх елементів. Якщо це зробити неможливо, видати повідомлення про причину.

11. Задано масив А(3,5). Отримати новий масив діленням усіх елементів початкового масиву на елемент масиву, найбільший по абсолютній величині. На друк вивести вхідний масив, новий масив та максимальний елемент. Елементи масиву А задати самостійно.

12. Задано двовимірний масив А(6,7). Визначити середнє арифметичне елементів цієї матриці, у яких сума індексів одночасно >7 і <11.

13. В двовимірному масиві знайти максимальний елемент із додатних елементів.

14. В квадратній матриці знайти середнє арифметичне з елементів, що розташовані над третім рядком та лівіше третього стовбчика.

15. Знайти мінімальний елемент під другим рядком квадратної матриці.

16. Знайти суму елементів другого рядка та суму елементів третього стовпчика і їх кількість в масиві С (М, Х).

17. Задано масиви чисел A(M), B(N), C(K). З елементів з непарними індексами створити масив D(X,X), (X=>2). Значення Х вибрати таким, щоб масив D мав максимально можливі розміри.

18. Задано масиви чисел A(M,N), B(L). Із кратних 3 елементів створити масив C(Y,Y) (Y=>2). Значення Y вибрати таким, щоб масив C мав максимально можливі розміри.

19. Задано масиви чисел X(M1,N1), Y(M2,N2). Із парних елементів створити два масиви A(K,K) та B(K,K), (K=>2). Значення К вибрати таким, щоб масиви А та В мали максимально можливі розміри.

20. Задано масиви чисел A(M), X1(M,N). З непарних елементів створити два масиви X(d,d) та Y(d,d), (d=>2). Значення d вибрати таким, щоб кількість непарних елементів, що не увійшли до створюваних масивів, було мінімальним.

21. Задано масиви чисел X(N), Y(N), Z(N). З елементів, кратних 5, що стоять на парних місцях, створити масив D(Y,Y), із останніх елементів — одновимірний масив F. Значення Y, (Y=>2) вибрати таким, щоб масив D мав максимально можливі розміри.

22. Задано масиви чисел В(Z,K) и C(N). З ненульових парних елементів створити масив A(X,X), (X=>2), з останніх елементів — одновимірний масив. Значення X, вибрати таким, щоб розмір масиву А був максимально можливим.

23. Дано масив чисел A(M). Створити з його елементів двовимірний масив В, в кожному рядку якого є К елементів. Недостаючі елементи останнього рядка масиву В заповнити одиницями.

24. Задано масив чисел X(N). Створити із його елементів двовимірний масив Y, в кожному стовпчику якого міститься А елементів. Якщо для останнього стовпчика елементів буде недостатньо, заповнити їх нулями.