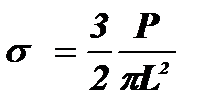Напружений стани гірських порід при втискуванні
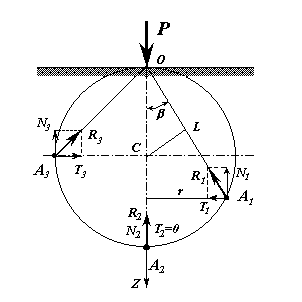
Розглянуті вище схеми взаємодії елементів озброєння доліт з породою показали, що руйнування породи відбувається послідовним деформуванням окремих ділянок поверхні вибою при одночасній дії нормальних і дотичних навантажень. Елементи озброєння сучасних доліт можуть мати різну конфігурацію робочої поверхні. В одних випадках – це різці з плоскою або заокругленою поверхнею ріжучої кромки, в других – це зубці у вигляді клину з плоскою або заокругленою вершиною, в третіх – штирі зі сферичною головкою. Звідси й виникли три задачі про розподіл напружень в пружному твердому тілі: 1) розподіл напружень при втискуванні індентора з плоскою робочою поверхнею; 2) розподіл напружень при втискуванні індентора зі сферичною робочою поверхнею; 3) розподіл напружень при втискуванні індентора з циліндричною робочою поверхнею. Загального рішення задачі про напружений стан гірських порід в процесі буріння немає. Однак, для якісного розгляду напруженого стану можна скористатися розв’язками для ідеалізованих схем навантаження з припущенням, що гірська порода ізотропна, деформується за законом Гука, а її пружні характеристики не залежать від напруженого стану і швидкості навантаження. Такі задачі розв’язуються на основі теорії Буссінеска. Теорія Буссінеска полягає у визначенні закону розподілу напружень і деформацій при дії зосередженої сили, прикладеної на поверхні лінійно деформованого масиву, обмеженого площиною, безмежний в усіх інших напрямах (рис. 10.3).
Рисунок 10.3 − Розрахункова схема до задачі Буссінеска Нехай сила прикладена нормально до поверхні в точці О. Згідно теорії Буссінеска радіальні напруження sR в масиві, зумовлені дією сили P, можна визначити так:
де Вертикальну складову цих напружень sN знаходять з виразу:
де
Не вдаючись до детального аналізу і розв’язку сформульованої задачі зупинимося на практичних висновках, які випливають з неї. 1 Якщо через точку прикладення зосередженої сили і деяку точку пружного на півпростору провести сферу з центром на лінії дії прикладеної сили, то в будь-якій точці на сфері буде діяти рівна за модулем реакція 2 Складові реакції нормальна
3 З формули (10.4) випливає, що поблизу точки прикладення сили стискуючі напруження прямують до безмежності. Тому ця формула справедлива лише на деякій відстані від точки прикладення сили. Розміри області, для якої формула неадекватна, можуть бути визначені з теорії пластичності. 4 Якщо на пружний півпростір діє кілька зосереджених сил, загальна реакція в будь-якій точці півпростору є геометричною сумою реакцій від кожної сили зокрема. Тангенціальні складові окремих реакцій можуть взаємно компенсуватися, нормальні ж складові завжди сумуються, збільшуючи силу відриву (див. рис. 10.4).
Рисунок 10.4 − Розподіл напружень при дії двох зосереджених сил
|

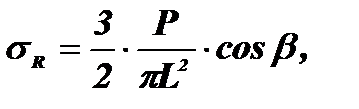 (10.4)
(10.4) .
.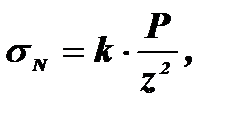 (10.5)
(10.5)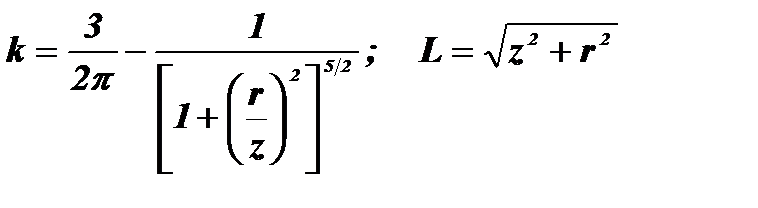
 , спрямована в точку прикладення зусилля.
, спрямована в точку прикладення зусилля. і тангенціальна
і тангенціальна 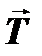 мають різні співвідношення, величина яких залежить від положення точки на сфері. На осі симетрії при b=0 всі нормальні напруження стискуючі, тобто при дії зосередженої сили має місце усесторонній стиск:
мають різні співвідношення, величина яких залежить від положення точки на сфері. На осі симетрії при b=0 всі нормальні напруження стискуючі, тобто при дії зосередженої сили має місце усесторонній стиск: