для нахождения максимального потока
Данные: транспортная сеть D, заданная матрицей пропускных способностей дуг. Результат: максимальный поток в сети.
1. Построить произвольный поток φ на транспортной сети D (например, положить φ(u) = 0 для любой дуги u). 2. Просмотреть пути, соединяющие вход сети v1 с выходом vn. Если поток φ полный, то перейти к п.4. 3. В противном случае рассмотреть путь μ, соединяющий вход сети v1 с выходом vn, все дуги которого не насыщены. Построить новый поток φ´:
где 4. Присвоить целочисленные метки вершинам сети D и знаки «+» или «-» дугам по правилам: · входу v1 присвоить метку 0, · если вершина vi получила некоторую метку, а y - еще непомеченная вершина, то вершине y · повторять процесс, описанный в предыдущем пункте до тех пор, пока не прекратится появление новых отмеченных вершин и дуг. Если в результате выполнения этого пункта вершина vn не получит метки, то поток является максимальным. В противном случае перейти к п.5. 5. Рассмотреть последовательность отмеченных вершин λ=(vn, vi1, vi2,…,v1), каждая из которых имеет метку, равную номеру последующей вершины, и последовательность μ (не обязательно путь), соединяющих последовательные вершины из λ. Построить новый поток φ´:
Перейти к пункту 4.
Пример. Рассмотрим транспортную сеть D и полный поток φ, для которого
2
7 (8) 7 (7)
0(1,+) 5 (3,+) 6 (4,+)
3 (3) 10 (10) 0 (3) 13 (15)
4 (5,+) Рис. 1.
Присвоим вершине 1 метку 0, тогда вершине 2 присвоим метку (1,+), т.к. φ((1,2))<c((1,2)). Т.к. φ((2,5))=c((2,5)), то переходим к вершине 3, которой присвоим метку (1,+), затем вершине 5 – (3,+), вершине 4 – (5,+), вершине 6 – метку (4,+). Рассмотрим последовательность вершин λ=(6,4,5,2,1), и построим новый поток, величина которого равна 15.
2
7 (8) 7 (7)
0 5 6 1 5 (5) 3 7 (7) 1 (1)
3 (3) 10 (10) 1 (3) 14 (15)
4 Рис. 2. Нетрудно заметить, что улучшить данный поток нельзя.
|


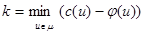 . Повторить этот процесс до получения полного потока φ.
. Повторить этот процесс до получения полного потока φ. Гvi, такой что φ((vi,y))<c((vi,y)) присвоить метку i, а дуге (vi,y) – знак «+»; вершине y
Гvi, такой что φ((vi,y))<c((vi,y)) присвоить метку i, а дуге (vi,y) – знак «+»; вершине y 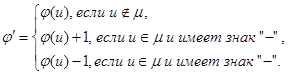
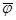 = 14:
= 14: (1,+)
(1,+)