Решение. . Отбросив заделки и заменив их действие на стержень реактивными моментами Мм и М1В, получим эквивалентную систему
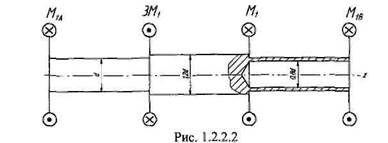
Отбросив заделки и заменив их действие на стержень реактивными моментами Мм и М1В, получим эквивалентную систему, которая должна находиться в равновесии (рис. 1.2.2.2).
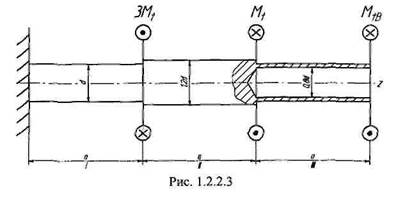
В единственное уравнение равновесия входят два неизвестных фактора,следовательно, задача один раз статически неопределима. Необходимо составить одно дополнительное уравнение перемещения. Для этого в исходной системе отбросим правую заделку, заменим ее реактивным моментом Мв и определим этот момент из условия <рв = 0, выражающего тот факт, что опора представляет собой жесткую заделку (рис. 1.2.2.3). Представим уравнение перемещения в виде 22 Глава 1 Сопротивление материалов Далее, по аналогии с задачей 1.2.1, разобьем стержень на участки /—/// и найдем геометрические характеристики (полярные моменты инерции и полярные моменты сопротивления) каждого участка:
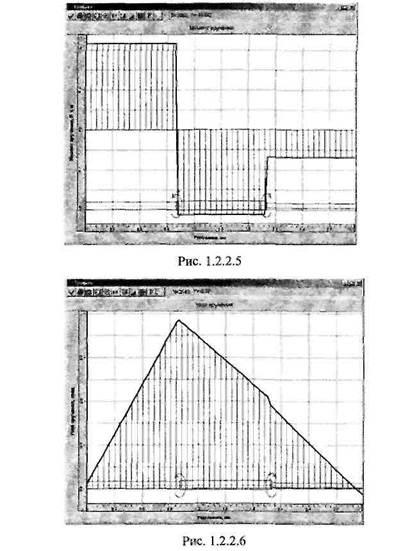
Зная реакции в опорах и воспользовавшись методом сечений, легко построить эпюры моментов кручения, наибольших касательных напряжений и углов поворота. Результаты построения эпюр моментов М,, максимальных касательных напряжений Решение задачи в модуле АРМ Beam Данная задача решается аналогично задаче 1.2.1. На рис. 1.2.2.5 и 1.2.2.6 представлены эпюры моментов кручения и углов поворота поперечных сечений, построенные с помощью модуля АРМ Beam. Возможно-
24 Глава 1 Сопротивление материалов
сти этой программы позволяют получить также карту распределения напряжений по сечению для любого сечения стержня. На рис. 1.2.2.7 показано распределение напряжений для одного из сечений участка //. ИЗГИБ
|

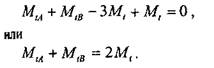



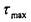 и углов закручивания
и углов закручивания 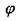 приведены на рис. 1.2.2.4.
приведены на рис. 1.2.2.4.