Решение. Рассматриваемая задача является один раз статически неопределимой, поскольку из единственного уравнения равновесия найти двенеизвестные реактивные силы
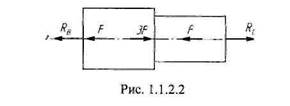
Рассматриваемая задача является один раз статически неопределимой, поскольку из единственного уравнения равновесия найти две неизвестные реактивные силы невозможно. Статически неопределимые задачи решаются дополнением статического уравнения равновесия необходимым количеством уравнений перемещений, отражающих особенности наложенных на деформируемую систему геометрических связей. В данной задаче действие опор описываем реактивными силами RB и Rc (рис. 1.1.2.2). Тогда уравнение равновесия имеет вид RB-RC + F + F-3F = 0=> RB=RC + F.
Уравнение равновесия в данном случае необходимо дополнить одним уравнением перемещений. Для записи уравнения перемещений можно использовать одно из двух
12 Глава 1. Сопротивление материалов граничных условий, следующих из жесткой заделки обоих концов стержня: Воспользуемся граничным условием нив ее действие на стержень реакцией Rc, получим статически определимый стержень, нагруженный кроме заданных сил неизвестной силой Rc (рис. 1.1.2.3). Применив принцип независимости действия сил, представим уравнение перемещений в виде
где грузки Пользуясь законом Гука, запишем выражение для перемещений от активных и реактивных сил:
1.1. Растяжение — Сжатие 13 Эпюры продольных сил N и нормальных напряжений Перемещение сечения /— 1 найдем так же, как в задаче 1.1.1:
Решение задачи в модуле АРМ Beam Расчет стержней в модуле АРМ Beam несколько отличается от их расчета в АРМ Structure3D (см. задачу 1.1.1). Дело в том, что, в отличие от АРМ Structure3D, в котором силовой фактор можно задать только в узловой точке, в АРМ Beam допускается приложение силы в любой точке участка стержня. Применительно к рас-
сматриваемой задаче это означает, что для ее решения необходимо создать всего два стержня, отличающихся между собой формой поперечного сечения. Окно результатов расчета показано на рис. 1.1.2.5. Некоторые из кнопок (графики результатов) могут быть недоступны. Это определяется выбором типа расчета (статический расчет, изгибные колебания в вертикальной плоскости, изгибные ко- 14 Глава 1. Сопротивление материалов лебания в горизонтальной плоскости, крутильные колебания) в меню «Расчет: типы расчета». Ниже приведено решение рассматриваемой задачи, выполненное в модуле АРМ Beam. На рис. 1.1.2.5 и 1.1.2.6 представлены эпюры осевых сил и напряжений. Пе-
1.1. Растяжение — Сжатие 15 ремещение сечения 1 —1 можно найти как по графику перемещений (рис. 1.1.2.7),так и при помощи таблицы 1.1.2.1 с уточненными значениями перемещений; фрагмент этой таблицы, содержащей искомое сечение (сечению 1—1 соответствует точ-
ка на оси абсцисс с расстоянием 800 мм от левого конца балки), располагается после графика. Таблица 1.1.2.1. Перемещение в осевом направлении
|


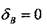 или
или 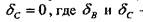 — перемещения сечений В и С соответственно.
— перемещения сечений В и С соответственно. Отбросив правую заделку и заме-
Отбросив правую заделку и заме-
 — перемещение сечения С вследствие действия приложенной внешней на-
— перемещение сечения С вследствие действия приложенной внешней на- — перемещение сечения С вследствие действия реактивной силы Rc.
— перемещение сечения С вследствие действия реактивной силы Rc.
 строим по известным значениям активных и реактивных силовых факторов. Это легко сделать с помощью метода сечений. Построенные эпюры приведены на рис. 1.1. 2.4.
строим по известным значениям активных и реактивных силовых факторов. Это легко сделать с помощью метода сечений. Построенные эпюры приведены на рис. 1.1. 2.4.