Решение. Для того чтобы ответить на поставленные вопросы, необходимо воспользоваться методом сечений
Для того чтобы ответить на поставленные вопросы, необходимо воспользоваться методом сечений. В рассматриваемом случае крутящий момент, возникающий в произвольном поперечном сечении стержня, численно равен алгебраической сумме крутящих моментов, приложенных к отсеченной части. Крутящий (вращающий) момент будем считать положительным, если для наблюдателя, смотрящего из конца вектора нормали на плоскость поперечного сечения, момент представляется направленным против хода часовой стрелки. Таким образом, используя метод сечений и правило знаков, строим эпюру крутящих моментов (рис. 1.2.1.2). Прежде чем переходить к построению эпюры максимальных касательных напряжений, необходимо в каждом из заданных поперечных сечений рассчитать полярный момент сопротивления кручению. Для удобства дальнейших вычислений разобьем стержень на участки I—IV, характеризующиеся постоянным значением крутящего момента и неизменной формой поперечного сечения, и вычислим полярный момент сопротивления каждого участка: 1.2. Сдвиг и кручение 17
Эпюру максимальных касательных напряжений (рис. 1.2.1.2) строим по рассчитанным величинам момента кручения и соответствующим им значениям полярного момента сопротивления (2.4.24), rmax =M,IWP.
Угол закручивания участка стержня, имеющего постоянное поперечное сечение, при условии, что момент кручения во всех сечениях данного участка одинаков, определяется по формуле 2.4.25:
18 Глава 1 Сопротивление материалов Вычислим полярные моменты инерции для каждого из участков стержня:
Эпюру углов поворота сечений угол поворота сечения А:
угол поворота сечения В:
Решение задачи в модуле АРМ Beam На рис. 1.2.1.3 и 1.2.1.4 показаны эпюры моментов кручения и углов поворота поперечных сечений, полученные при решении данной задачи в модуле АРМ Beam. Эта программа позволяет также получить эпюру эквивалентных напряжений, которая здесь не представлена. Зная величины эквивалентных напряжений, можно,используя энергетическую теорию прочности, легко перейти к максимальным каса- 1.2. Сдвиг и кручение 19
|

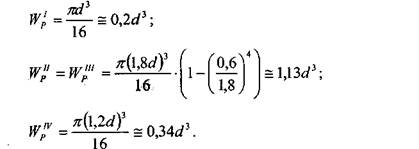

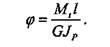
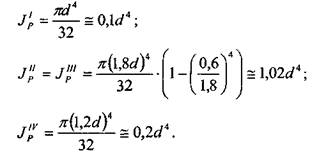
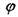 строим, начиная от закрепленного конца. В пределах каждого из участков стержня эпюра углов линейна,поэтому достаточно найти углы поворота только для граничных сечений участков:
строим, начиная от закрепленного конца. В пределах каждого из участков стержня эпюра углов линейна,поэтому достаточно найти углы поворота только для граничных сечений участков: , т. к. это сечение закреплено;
, т. к. это сечение закреплено;



