Статически определимая система

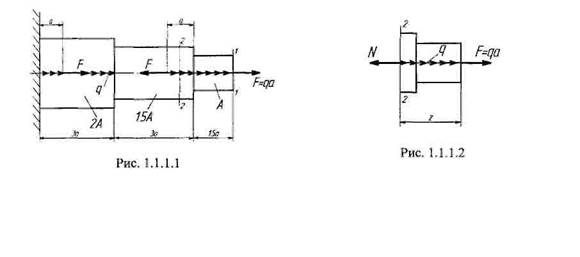
Построить эпюры продольных сил и нормальных напряжений для состоящего из участков различного поперечного сечения стержня, находящегося под действием равномерно распределенной нагрузки q и сосредоточенных сил F (рис. 1.1.1.1). Вычислить перемещение сечения /—/.

Принять: А = 4 см²; q = 40 кН/м; а = 0,2 м;

F = qa = кH; £ = 2 10⁵МПа.

Решение

Эпюру продольных сил строим методом сечений [5], который заключается в следующем: стержень в произвольной точке рассекается поперечной плоскостью, действие отсеченной части заменяется реактивными силами, а затем рассматрива­ется равновесие отсеченной части.

Если заданный по условию стержень рассекается по сечению 2 — 2, то, согласно рис. 1.1.1.2, уравнение равновесия запишется в виде

N = F + qz = qa + qz, где N — продольная сила в сечении 2 — 2.

_8_____________________________ Рассмотрев условия равновесия отсеченной части для каждого из указанных выше сечений стержня, получим эпюру продольных сил (рис. 1.1.1.3). Считаем, что при центральном растяжении (сжатии) нормальные напряжения равномерно распреде­лены по плошали поперечного се-

где N. — продольная сила в рас­сматриваемом /-ом сечении; А, — площадь текущего попереч­ного сечения. Таким образом, эпюру нормальных напряжений можно получить делением вели­чины продольной нагрузки на площадь соответствующего попе­речного сечения (рис. 1.1.1.3).

Полное перемещение произ­вольного сечения равно алгебраи­ческой сумме перемещений от ка­ждого из силовых факторов в от­дельности. Его можно вычислить по формуле, которая следует из

1.1. Растяжение — Сжатие 9

Решение задачи в модуле АРМ Structure3D

Для выполнения необходимых вычислений в программном модуле АРМ Struc- ture3D стержень разбивается на необходимое количество участков (в данном слу­чае — на 5 участков) с помощью узлов. Узлы помещаются на концах стержня, в местах изменения поперечного сечения и в точках приложения сосредоточенных нагрузок. Номера узлов показаны на диаграмме осевой силы, а номера стержней, для большего удобства при сопоставлении результатов теоретического расчета и расчета в АРМ Structure3D, отмечены на самом стержне (рис. 1.1.1.3).

Следует отметить, что возможности АРМ Structure3D позволяют помимо таб­личных результатов получать также цветовые карты результатов для внутренних нагрузок, напряжений и перемещений с варьируемым числом изоуровней (здесь эти карты не приведены). Перемещение сечения 1 —/ в рассматриваемом случае можно определить либо из цветовой карты результатов, либо как максимальное перемещение всего стержня в целом (сечение 1—1 расположено на конце стержня, и его перемещение будет наибольшим).

Замечание. При автоматизированном расчете с помощью АРМ Structure3D полу­ченный результат относится к локальной системе координат стержня [4], кото­рая жестко привязана к его началу и организована следующим образом: ось X всегда располагается вдоль стержня, ось Y направлена вертикально вверх, а ось Z дополняет систему координат до правой тройки.

Ясно, что в локальной системе координат стержня все параметры рассматривае­мой задачи, кроме осевых (направленных вдоль оси X), равны нулю.

Результаты расчета в АРМ Structure3D