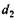Условие прочности по контактным напряжениям имеет вид 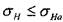 , где
, где
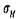 — действующее напряжение в контакте зубьев, а
— действующее напряжение в контакте зубьев, а  — допускаемое. Про-
— допускаемое. Про-
верка выполнения этого условия сводится к определению величины напряжений в контакте зубьев (7.1.81) и сравнению полученных значений с допускаемыми напряжениями:
Следовательно, условие прочности по напряжениям контакта для проектируемой передачи можно считать выполненным.
140 Глава 3. Передаточные механизмы
Пользуясь формулой (7.1.91) для расчета коэффициента формы зуба 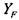 , ,
|
| для шестерни и колеса соответственно получаем:
|
Проверка выполнения условия прочности по напряжениям изгиба Вначале определяем приведенное число зубьев (7.1.101) шестерни и колеса:
Используя полученные величины коэффициентов формы зуба, переходим к расчету напряжений изгиба (7.1.102) и проверке изгибной прочности зубьев:

где коэффициент учета осевого перекрытия  определяется по формуле 7.1.103, а именно:
определяется по формуле 7.1.103, а именно: 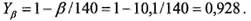 Тогда для шестерни и колеса соот-
Тогда для шестерни и колеса соот-
ветственно имеем:
Как видно из сравнительных соотношений, условие прочности по напряжениям изгиба для проектируемой передачи можно считать выполненным.
3.1. Проектировочный расчет зубчатой цилиндрической косозубой передачи 141
Геометрические размеры зубчатой передачи в случае нарезания зубчатых колес без смещения (таблица 7.1.3)
Диаметры вершин зубьев шестерни  и колеса и колеса 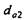
|
Диаметры впадин зубьев шестерни 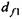 и колеса и колеса 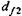 : :
|
Диаметры делительной и начальной окружностей шестерни  и колеса
и колеса 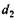

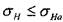 , где
, где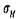 — действующее напряжение в контакте зубьев, а
— действующее напряжение в контакте зубьев, а  — допускаемое. Про-
— допускаемое. Про-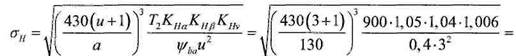

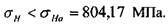
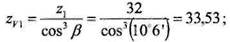
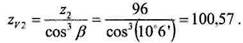
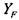 ,
,


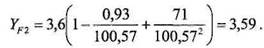

 определяется по формуле 7.1.103, а именно:
определяется по формуле 7.1.103, а именно: 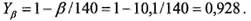 Тогда для шестерни и колеса соот-
Тогда для шестерни и колеса соот-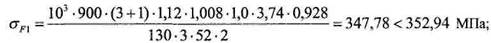

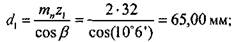
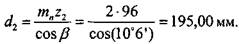
 и колеса
и колеса 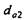

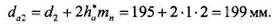
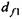 и колеса
и колеса 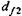 :
:
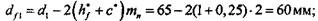
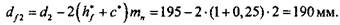
 и колеса
и колеса