б) Информационная неопределенность задачи
Проблема 4. Позиционирование машины Поста на последнюю помеченную ячейку Пусть на ленте машины Поста заданы наборы помеченных ячеек (кортежи) произвольной длины с произвольными расстояниями между кортежами, и головка находится у самой левой помеченной ячейки. Задача состоит установке головки на самую правую помеченную ячейку последнего кортежа. Попытка построения алгоритма, решающего эту задачу приводит к необходимости ответа на вопрос – когда после обнаружения конца кортежа мы сдвинулись вправо по пустым ячейкам на М позиций и не обнаружили начало следующего кортежа – больше на ленте кортежей нет или они есть где-то правее? Информационная неопределенность задачи состоит в отсутствии информации либо о количестве кортежей на ленте, либо о максимальном расстоянии между кортежами – при наличии такой информации (при разрешении информационной неопределенности) задача становится алгоритмически разрешимой.
в) Логическая неразрешимость (в смысле теоремы Гёделя о неполноте)
Проблема 5. Проблема «останова» (см. теорему); Проблема 6. Проблема эквивалентности алгоритмов; По двум произвольным заданным алгоритмам (например, по двум машинам Тьюринга) определить, будут ли они выдавать одинаковые выходные результаты на любых исходных данных. Проблема 7. Проблема тотальности; По произвольному заданному алгоритму определить, будет ли он останавливаться на всех возможных наборах исходных данных. Другая формулировка этой задачи – является ли частичный алгоритм Р всюду определённым?
В качестве более подробного примера алгоритмически неразрешимой задачи рассмотрим проблему соответствий Поста (Э. Пост, 1943 г.). Мы выделили эту задачу, поскольку на первый взгляд она выглядит достаточно «алгоритмизуемой», однако она сводима к проблеме останова и является алгоритмически неразрешимой.
Проблема 8. Проблема соответствий Поста над алфавитом Постановка задачи. Пусть дан алфавит Проблема. Выяснить, существует ли конечная последовательность этих пар, не обязательно различных, такая что цепочка, составленная из левых подцепочек, совпадает с последовательностью правых подцепочек – такая последовательность называется решающей. В качестве примера рассмотрим 1. Входные цепочки: (abbb, b), (a, aab), (ba, b). Решающая последовательность для этой задачи имеет вид:
(a, aab) (a, aab) (ba, b) (abbb, b), так как: a a ba abbb
2. Входные цепочки: (ab, aba), (aba, baa), (baa, aa). Данная задача вообще не имеет решения, так как нельзя начинать с пары (aba, baa) или (baa, aa), поскольку не совпадают начальные символы подцепочек, но если начинать с цепочки (ab, aba), то в последующем не будет совпадать общее количество символов «а», т.к. в других двух парах количество символов «а» одинаково. В общем случае мы можем построить частичный алгоритм, основанный на идее упорядоченной генерации возможных последовательностей цепочек (отметим, что мы имеем счетное множество таких последовательностей) с проверкой выполнения условий задачи. Если последовательность является решающей – то мы получаем результативный ответ за конечное количество шагов. Поскольку общий метод определения отсутствия решающей последовательности не может быть указан, т.к. задача сводима к проблеме «останова» и, следовательно, является алгоритмически неразрешимой, то при отсутствии решающей последовательности алгоритм порождает бесконечный цикл.
В теории алгоритмов такого рода проблемы, для которых может быть предложен частичный алгоритм их решения, частичный в том смысле, что он возможно, но не обязательно, за конечное количество шагов находит решение проблемы, называются частично разрешимыми проблемами.
В частности, проблема останова так же является частично разрешимой проблемой, а проблемы эквивалентности и тотальности не являются таковыми.
|


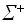 х
х  , ……,
, ……,  .
. aab aab b b
aab aab b b


