Расчеты тепловых полей.
Под действием вводимой в металл тепловой энергии различные его участки изменяют температуру. Температура будет меняться в пространстве и во времени. Для ее оценки можно, конечно, взять общее дифференциальное уравнение теплопроводности:
и, добавив граничные условия, решать его численно для конкретного случая (с помощью, например метода конечных разностей или др.). В подвижной системе координат это уравнение примет вид:
Даже на современных машинах такое решение может оказаться весьма длительным, а в некоторых случаях и не возможным, т.к. с, r, λ – также зависят от температуры, и зависимость носит сложный (не линейный) характер, в том числе в результате полиморфных превращений, например для титана в интервале температур 1200…1700 оС λ почти в 5 раз. Кроме того, имеющиеся справочные данные справедливы для изотермических условий, т.е. когда температура зафиксирована. В реальных условиях сварки динамика изменения температур высока, появляются поля напряжений и деформаций, и реальные зависимости теплофизических характеристик от температуры отличаются от справочных Т.о. точность (достоверность) таких расчетов во многом зависят от достоверности вводимых данных. Выполнять такие расчеты долго и дорого. Поэтому для практических расчетов часто используются частные аналитические решения для упрощенных моделей или расчетных схем. Модели источников теплоты: - Точечный источник – его объём бесконечно мал, все тепло вводится в одну точку. - Линейный источник – все тепло равномерно распределено по цилиндру с r = 0, т.е. в линию. - Плоский источник – равномерно распределенный по некоторой конечной плоскости (например, торец стержня). - Объёмный источник – равномерно выделяющий тепло в некотором объёме, например при протекании тока в стержне электрода. - Нормально-круговой распределенный источник на поверхности. - Мгновенный источник – длительность действия его стремится к «0». - Непрерывно действующий источник – источник постоянной тепловой мощности действующий достаточно долго. - Периодически действующий источник - Неподвижный источник – не перемещающийся источник постоянной мощности v = 0. - Подвижный источник – v ¹ 0. - Быстродействующий источник – распространение тепла впереди источник отсутствует (им можно пренебречь). Модели тела (основные): 1. Бесконечное тело. 2. Полубесконечное тело. 3. Плоский слой – учитывается отражение тепла от нижней и верхней границы тела. 4. пластина – тепло не распространяется перпендикулярно поверхностям, а только параллельно им. 5. Стержень – тепло распространяется вдоль стержня равномерно по всему сечению. В 1951 году Н.Н. Рыкалин опубликовал монографию «Расчет тепловых процессов при сварке», в которой предложил аналитические решения для некоторых расчетных схем из которых (как наиболее часто используемые) можно назвать: 1. Точечный непрерывный источник на поверхности полубесконечного тела. 2. Линейный источник (подвижный, непрерывный) в пластине. 3. Точечный источник на поверхности плоского слоя. 4. Быстродвижущийся источник на поверхности плоского слоя. 5. Плоский источник на торцевой поверхности стержня. Компьютеров тогда не было и даже калькуляторов, поэтому даже полученные аналитические выражения были весьма трудоемки. Для решения инженерных задач были составлены специальные графики – Номограммы – с помощью которых можно было графически получать решение некоторых сложных функций. (см. Петров, Тумарев) С появлением вычислительной техники пользование номограммами и таблицами функций стало не удобным. Поэтому В.А. Кархиным были предложены аналитические решения для известных и некоторых новых расчетных схем. Возьмем для примера: 1.Подвижный точечный источник на полубесконечном теле: (уравнение для установившегося режима в подвижной системе координат) Т(x,R,t®∞) = 2. Подвижный линейный источник в бесконечной пластине. (например, для лазерной и электроннолучевой сварки с полным проваром) Т(x,r,t®∞) = К 0 – модифицированная функция Бесселя второго рода нулевого порядка,(имеется представление в виде ряда); b – коэф. теплоотдачи с поверхности. 3. Подвижный объёмный источник, распределенный произвольно по толщине бесконечного плоского слоя и нормально в плоскости параллельной поверхности слоя:
где t 0 = R э2/4 a; R э – эффективный радиус пятна нагрева; q 1(z) – функция распределения интенсивности источника нагрева по толщине; s – толщина плоского слоя. Так для нормально-кругового закона Rэ = В данном уравнении отсутствует требование установившегося поля. (Для повехн. ист. z = 0, т.е. второй интегр. = Qэ; для линейного распределения по глубине q 1(z) = 0, т.е. интеграл и весь бесконечный ряд = 0; если внести Qэ под интеграл и задать закон его изменения, можно рассматривать функцию для пульсирующего источника) 4. Кроме того построены зависимости для стержня, для цилиндра, для периодического источника, и др. (См. В.А. Кархин)
|

 = div(λ grad T) + q уд, (q уд – источник теплоты (сток)(объемный), действующий в элементарном объеме, с объемной плотностью мощности (удельной мощностью) Вт/м3)
= div(λ grad T) + q уд, (q уд – источник теплоты (сток)(объемный), действующий в элементарном объеме, с объемной плотностью мощности (удельной мощностью) Вт/м3)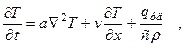 где
где 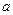 = λ / c ρ, м2 / с; Ñ - оператор Лапласа.
= λ / c ρ, м2 / с; Ñ - оператор Лапласа.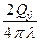 exp(-
exp(-  )
) 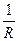 exp(-
exp(- 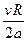 ), где R =
), где R = 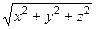
 , где r =
, где r = 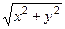 ;
;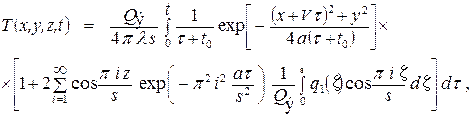
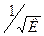 .
.


