Сверхпроводимость
Лекция 17
Сверхпроводимость была открыта в 1911 году голландским физиком Камерлинг-Оннесом. Изучая зависимость сопротивления ртути от температуры, он установил, что при очень низких температурах сопротивление образца исчезало. При температуре 4,2 К удельное электрическое сопротивление резко обращалось в ноль. Согласно теории электропроводности металлов в образцах без примесей и дефектов удельное сопротивление должно стремиться к нулю при понижении температуры (Т →0 К) постепенно.
металлических элементов, большого числа металлических соединений и при некоторых условиях у ряда полупроводников. Температура Т с, называемая температурой сверхпроводящего перехода или критической температурой, при которой у образца исчезает сопротивление, для разных веществ представлена в таблице.
При Т < Тс сопротивление сверхпроводников равно нулю. Это означает, что если через сверхпроводящее кольцо пропустить ток и отключить это кольцо от источника, то ток будет сохраняться в кольце сколь угодно долго. Изучение кристаллической структуры сверхпроводника показало, что при температурах, меньших критической T c, не происходит никаких изменений в кристаллической решетке. Свойства твердого тела, зависящие от колебаний кристаллической решетки, также остаются неизменными. Таким образом, сверхпроводимость не связана с какими-либо изменениями кристаллической структуры. Теплоемкость несверхпроводящего металла, как известно, в области низких температур складывается из теплоемкостей кристаллической решетки и электронного газа, температурная зависимость теплоемкости имеет вид: Охлаждение сверхпроводника приводит к тому, что при критической температуре (Т=Тс) происходит скачок теплоемкости без появления скрытой теплоты, т.е. имеет место фазовый переход второго рода. При температурах ниже критической (Т < Тс) зависимость теплоемкости от температуры определяется выражением вида: -решеточный вклад в теплоемкость остается без изменений, а электронный меняется, т.е. сверхпроводимость связана с какими-то коренными изменениями поведения электронов проводимости. В 1950 г. Максвеллом и независимо Рейнольдсом было установлено, что образцы сверхпроводника, изготовленные из разных изотопов одного и того же элемента, обладают различными критическими температурами. В большинстве случаев критическая температура обратно пропорциональна корню квадратному из массы изотопа. Это изотопический эффект. Он свидетельствует о том, что хотя кристаллическая решетка при переходе в сверхпроводящее состояние и не изменяется, она играет существенную роль в изменении свойств электронного газа. Для явления сверхпроводимости существенным является взаимодействие электронов с колебаниями решетки. Мейсснер и Оксенфельд установили, что если образец сверхпроводника охлаждать в магнитном поле до температуры ниже критической, то в точке сверхпроводящего перехода магнитное поле выталкивается из образца, т.е. в сверхпроводнике магнитная индукция В =0 – сверхпроводник является идеальным диамагнетиком (это эффект Мейсснера-Оксенфельда). Этот результат не является просто следствием исчезновения сопротивления. Действительно, согласно закону Ома При конечном значении плотности тока Тогда, согласно уравнению Максвелла Таким образом, идеальный диамагнетизм, также как и нулевое сопротивление - это фундаментальное свойство сверхпроводника. По своим магнитным свойствам все сверхпроводники делятся на сверхпроводники первого и второго рода. · Эффект Мейсснера - Оксенфельда наблюдается у сверхпроводников первого рода, к которым относятся все сверхпроводники, кроме ниобия. · Сверхпроводники второго рода (ниобий, сверхпроводящие сплавы и химические соединения) не обнаруживают эффекта Мейсснера – Оксенфельда, хотя магнитное поле в них и проникает. Сверхпроводимость можно разрушить магнитным полем с напряженностью больше некоторой критической Нс, которая зависит от температуры следующим образом:
Эффекты Джозефсона. В 1962 году Джозефсон предсказал эффекты слабой сверхпроводимости. Различают стационарный и нестационарный эффекты Джозефсона. · Стационарный эффект заключается в том, что сверхпроводящий ток может течь в отсутствие электрического поля через щель между двумя сверхпроводниками, заполненную изолятором, если толщина слоя изолятора достаточно мала (1-2 нм). Это означает, что “сверхпроводящие” электроны способны туннелировать через тонкие изолирующие слои. · Если увеличить ток через подобный контакт сверхпроводников, то он достигнет некоторого максимального значения, после чего на контакте появится электрическое напряжение V. Согласно предсказаниям Джозефсона, в этих условиях на контакте должен появиться высокочастотный переменный ток с частотой Это нестационарный эффект Джозефсона. Эффекты Джозефсона подтверждены экспериментально и положены в основу чрезвычайно точного метода измерения напряжения. Эффекты Джозефсона подтверждают согласованное когерентное поведение электронов, объединившихся в единый квантовый коллектив. Еще в 30-х годах указывалось на то, что сверхпроводящее состояние может быть разрушено с помощью электромагнитного излучения соответствующей частоты. При этом излучение должно быть поглощено сверхпроводником. Эксперимент подтвердил, что при температурах ниже критической (Т<Тс) поглощение электромагнитных волн возникает при частотах, больших 1011 Гц. Наличие “края поглощения” в сверхпроводниках свидетельствует о существовании в их спектре некоторой энергетической щели (~10-4 эВ). Если ширину этой щели выразить через Первой теорией, описавшей свойства сверхпроводников, была теория, созданная физиками Ф. и Г. Лондонами в 1935 году. Они основывались на двухжидкостной теории сверхпроводника. · При температурах ниже критической (Т<Тс) в сверхпроводнике имеются “сверхпроводящие” электроны с концентрацией · Плотность “сверхпроводящих” электронов · При приближении к абсолютному нулю (Т Теория Лондонов была ограниченной в силу ее феноменологичности. · Она не раскрывала природы сверхпроводников · и не объясняла, что представляют собой сверхпроводящие электроны. В теории Гинзбурга-Ландау для описания свойств сверхпроводников была привлечена квантовая механика. · Вся совокупность сверхпроводящих электронов описывалась волновой функцией Ψ;(r) от одной пространственной координаты. · Введением функции Ψ;(r) устанавливалось когерентное, согласованное поведение всех сверхпроводящих электронов (в случае “нормальных” электронов Ψ; является функцией п координат Ψ;= Ψ;(r 1, r 2… rn)). · В случае же сверхпроводника все Но эта теория также не была всеобъясняющей. Она не давала понимания явления сверхпроводимости на микроскопическом уровне. В 1957 году Дж.Бардин, Л.Купер и Дж.Шриффер опубликовали теорию (теория БКШ), раскрывающую микроскопический механизм сверхпроводимости. Вот основные результаты этой теории: 1. Притяжение между электронами. Итак, сверхпроводимость связана с некоторым изменением в поведении электронов проводимости. При этом кристаллическая решетка активно участвует в создании сверхпроводящего состояния (изотопический эффект). Одна из основных трудностей в создании теории сверхпроводимости заключалась в том, что было неясно, какое взаимодействие в системе электронов проводимости приводит к согласованному поведению электронов. Электроны проводимости в металле обладают энергиями в несколько электрон-вольт (~ EF), а сверхпроводящее состояние разрушается при Это взаимодействие осуществляется следующим образом. - В узлах кристаллической решетки металла находятся положительно заряженные атомные остовы. - Электрон стремится притянуть эти остовы, поэтому в окружающей электрон области происходит скопление положительных зарядов (т.е. под действием отрицательного заряда электрона решетка поляризуется). - Второй электрон, находящийся неподалеку, притягивается к поляризованной области, а, следовательно, к первому электрону. - Между электронами существует и кулоновское отталкивание, для сверхпроводника нужно, чтобы отталкивание было слабее притяжения. Электроны в металле обладают значительными скоростями, поэтому поляризация решетки не является статической. Возникающая при движении электрона поляризация зависит от того, насколько быстро решетка может откликаться на поляризующее воздействие электрона, т.е. поляризуемость решетки зависит от частоты собственных колебаний атомов. Взаимодействие электронов через решетку можно представить так. Один электрон испускает фонон, другой его поглощает. Рассмотрим металл при Т =0 К. При этой температуре фононов нет. Как происходит взаимодействие электронов? Пусть электрон имеет волновой вектор
В некоторый момент времени этот электрон возбуждает колебания решетки (испускает фонон), а сам переходит в состояние где Этот фонон почти мгновенно поглощается другим электроном, имеющим до взаимодействия квазиимпульс В результате поглощения фонона второй электрон переходит в состояние с квазиимпульсом
Таким образом, в результате обмена фононом электроны из состояний При этом Но рассеяние двух частиц может осуществляться только в случае их взаимодействия. Фонон, которым обмениваются электроны, называют виртуальным фононом. Он связан с поляризацией решетки и может существовать только при переходе от одного электрона к другому (в отличие от реального фонона). Виртуальные фононы не могут распространяться в решетке независимо от этих электронов. Чем сильнее в нормальном металле электрон-фононное взаимодействие, тем меньше его проводимость. Благородные металлы являются прекрасными проводниками. У них слабое электрон-фононное взаимодействие. Они не переходят в сверхпроводящее состояние даже при самых низких температурах. Все ли электроны притягиваются друг к другу? В процессе испускания фонона первый электрон переходит из состояния
Через фононы могут взаимодействовать лишь электроны, лежащие в достаточно узком сферическом слое Толщина слоя где Для электронов, имеющих энергию вне этого слоя, решетка движется слишком медленно и не успевает откликнуться на поляризующее действие электрона.
|


 Добавление примесей к ртути не приводило к появлению остаточного сопротивления, т.е. образцы также переходили в сверхпроводящее состояние.
Добавление примесей к ртути не приводило к появлению остаточного сопротивления, т.е. образцы также переходили в сверхпроводящее состояние.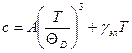 .
.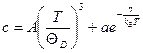
 .
. и удельном сопротивлении, стремящемся к нулю (
и удельном сопротивлении, стремящемся к нулю ( ), электрическое поле
), электрическое поле  в образце равно нулю.
в образце равно нулю.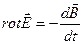 , должно быть
, должно быть 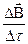 =0, т.е. магнитный поток в образце не может измениться при переходе в сверхпроводящее состояние.
=0, т.е. магнитный поток в образце не может измениться при переходе в сверхпроводящее состояние.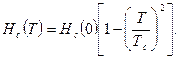
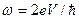 .
.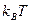 , то получается температура порядка ~ 1К. По порядку величины это соответствует критическим температурам сверхпроводящего перехода.
, то получается температура порядка ~ 1К. По порядку величины это соответствует критическим температурам сверхпроводящего перехода. (Т) и “нормальные” электроны с концентрацией
(Т) и “нормальные” электроны с концентрацией  , где n - полная концентрация электронов проводимости
, где n - полная концентрация электронов проводимости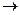 0 К)
0 К)  10-4 эВ. Таким образом, нужно было найти очень слабое взаимодействие электронов с участием решетки, приводящее к сверхпроводимости. Таким взаимодействием является притяжение между электронами, которое осуществляется через колебания решетки.
10-4 эВ. Таким образом, нужно было найти очень слабое взаимодействие электронов с участием решетки, приводящее к сверхпроводимости. Таким взаимодействием является притяжение между электронами, которое осуществляется через колебания решетки. .
. Его квазиимпульс
Его квазиимпульс 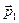 .
. с квазиимпульсом
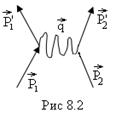
с квазиимпульсом  . При этом квазиимпульс системы сохраняется:
. При этом квазиимпульс системы сохраняется: 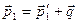 ,
, - квазиимпульс фонона (рис.8.2).
- квазиимпульс фонона (рис.8.2). .
. :
: .
.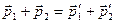 и
и  .
. . При этом состояние
. При этом состояние  Согласно принципу запрета Паули, такой переход возможен лишь вблизи уровня Ферми. Если представить состояния электрона в k -пространстве, то электронам, находящимся на уровне Ферми, соответствует
Согласно принципу запрета Паули, такой переход возможен лишь вблизи уровня Ферми. Если представить состояния электрона в k -пространстве, то электронам, находящимся на уровне Ферми, соответствует 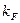 - поверхность, представляющая собой сферу (рис. 8.3).
- поверхность, представляющая собой сферу (рис. 8.3).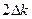 около поверхности Ферми. Остальные электроны не взаимодействуют.
около поверхности Ферми. Остальные электроны не взаимодействуют.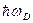 :
: 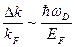 ,
, - энергия Ферми.
- энергия Ферми.


