Утверждение 4.
Пусть дана окружность с центром в точке (a, b) и радиусом R, тогда все точки, находящиеся вне данной окружности удовлетворяют неравенству
Алгоритм решения задачи:
Если для выполнения тех или иных действий нужно одновременное выполнение двух и более условий, то они объединяются логической связкой AND (И). Таким образом, условие данной задачи можно записать так: x^2+(y-1)^2<=1 AND y<=1-x^2 Программа CLS INPUT x, y IF x^2+(y-1)^2<=1 AND y<=1-x^2 THEN? “Да” ELSE? “Нет” END
Блочная форма оператора IF … THEN … ELSE Часто возникает необходимость в выполнении целой группы действий как в случае, если значение логического выражения — «истина», так и в случае, когда его значение — «ложь». Однако размещать несколько операторов в одной строке не рекомендуется: это значительно затрудняет зрительное восприятие текста программы и ее сложно понять. В таких случаях желательно использовать блочную форму условного оператора IF … THEN … ELSE.
IF {логическое выражение} THEN последовательность операторов, которая выполняется в том случае, если логическое выражение принимает значение «истинна» ELSE последовательность операторов, которая выполняется в том случае, если логическое выражение принимает значение «ложь» ENDIF
Алгоритм решения задачи: При решении данной системы возможны два случая. 1. Определитель системы
2. Если определитель системы a) если оба определителя b) если хотя бы один из определителей Программа 'Вводим значения коэффициентов построчно INPUT “a1, b1, c1=”;a1, b1, c1 INPUT “a2, b2, c2=”;a2, b2, c2 'Вычисляем определители det=a1*b2-a2*b1 detx=c1*b2-c2*b1 dety=a1*c2-a2*c1 IF det<>0 THEN x=detx/det: y=dety/det PRINT “Единственнон решение:” PRINT “x=”;x, “y=”;y ELSE IF detx=0 AND dety=0 THEN PRINT “Множество решений” ELSE PRINT “Нет решений” ENDIF ENDIF END
Введем обозначения:
 Алгоритм решения задачи: Алгоритм решения задачи:
Прежде чем приступать к написанию программы, необходимо записать аналитический вид данной функции. На промежутке Таким образом, функцию можно записать следующим образом:
Программа CLS INPUT "x="; x IF x < -2 THEN y = 8 ELSEIF x > 2 THEN y = (x-3)^2-9 ELSE y = -x ^ 3 END IF PRINT "y="; y END ü Оператор выбора SELECT… END SELECT Подобные длинные цепочки условных проверок можно записать и по-другому — с помощью оператора выбора, т. е. выбора нужного блока операторов и зависимости от истинности одного из нескольких условий. Этот оператор представляет условия значительно нагляднее, чем блочная расширенная форма оператора IF...THEN…ELSE. SELECT CASE {главное_выражение} CASE {список_тестовых_условий1} блок операторов -1 CASE {список_тестовых_условий2} блок операторов –2 … … …
|

 (рис.8).
(рис.8).

 Так как заштрихованная область находится внутри окружности
Так как заштрихованная область находится внутри окружности  , а также ниже графика функции
, а также ниже графика функции 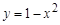 , то все точки данной области удовлетворяют одновременно двум условиям:
, то все точки данной области удовлетворяют одновременно двум условиям:  и
и  . Обратите внимание во втором условии записано нестрогое неравенство, т. к. точки самого графика
. Обратите внимание во втором условии записано нестрогое неравенство, т. к. точки самого графика 


 . Тогда система имеет единственное решение, которое находится по формулам Крамера:
. Тогда система имеет единственное решение, которое находится по формулам Крамера: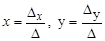 , где
, где 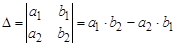


 , то возможны два подслучая:
, то возможны два подслучая: равны нулю, система имеет бесчисленное множество решений;
равны нулю, система имеет бесчисленное множество решений; не равен нулю, то система вообще не имеет решений.
не равен нулю, то система вообще не имеет решений.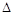 ,
,  ,
,  .
.


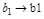








 функция имеет вид y=8, на промежутке
функция имеет вид y=8, на промежутке  функция имеет вид y=x3, на промежутке
функция имеет вид y=x3, на промежутке 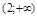 функция имеет вид
функция имеет вид  .
.




