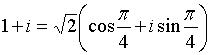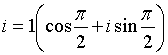П.2. Тригонометрическая форма записи комплексного числа.Комплексное число Тогда, комплексное число можно изобразить с помощью точки плоскости, координаты которой
Рис. 1. Тогда ось OX – где откладываются действительные части числа OY – где откладывают мнимые части числа Такую плоскость будем называть «комплексной плоскостью». Действительной и мнимой частям комплексного числа
Рис. 2. Т.е. комплексное число можно изобразить с помощью вектора Тогда, длина вектора Из определения модуля и аргумента следует, что если Тогда, любое комплексное число, отличное от нуля, можно представить в тригонометрической форме: Пример. Представить комплексное число в тригонометрической форме: 1) 2)
|
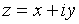однозначно определяется парой действительных чисел 
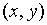поэтому можно установить взаимно однозначное соответствие между всевозможными точками плоскости и всевозможными комплексными числами.
- абсцисса, 
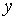- ордината. Это геометрическая, интерпретация комплексного числа.
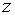называется действительной осью.
.
.
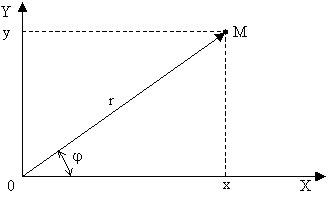
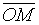- есть модуль комплексного числа 
; а угол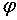 
есть аргумент комплексного числа:
.
, 
.
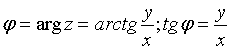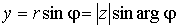