Примеры. 1. Определить область, заданную неравенствами: 2£ Im(z-i)£3
1. Определить область, заданную неравенствами: 2£ Im(z-i)£3. Перейдем к декартовым координатам, получим 2£ y-1£3Þ3£ y£ 4. Это область, заключенная в полосе между прямыми y=3 и y=4. 2. Определить область, заданную неравенством I z-i I<I z+3 I. Перейдем к декартовым координатам, получим Это часть плоскости, расположенная выше прямой y=-3x-4. 3. Определить область, заданную неравенством I z-3+2i I>2. Это часть плоскости, расположенная вне круга
Правило умножения двух комплексных чисел позволяет получить замечательное соотношение, открытое английским математиком А. де-Муавром (1667–1754). Найдем квадрат комплексного числа z = r(cos j + i sin j), т.е. результат произведения этого числа на само себя: z2 = z•z = r(cos j + i sin j)•r(cos j + i sin j). По правилу умножения двух комплексных чисел имеем: z2 = r2(cos j + i sin j)2 = r2(cos 2j + i sin 2j). Повторяя n раз операцию возведения в степень числа z, мы получим формулу n-ой степени числа z: zn = rn(cos nj + i sin nj), где n – натуральное число. Методом математической индукции можно доказать эту формулу. Она представляет собой обобщение формулы, открытой Муавром. Муавр открыл ее для случая, когда модуль комплексного числа z равен 1. Формула Муавра имеет вид: (cos j + i sin j)n = cos nj + i sin nj, где n Î N. С помощью формулы Муавра можно вывести многие полезные соотношения, в частности, между тригонометрическими выражениями. Формула Муавра позволяет найти значения корней любой (n-й) степени в поле комплексных чисел. Под корнем n-й степени из числа z понимают такое число a, n-я степень которого равна z: an = z. Ограничимся рассмотрением вопроса об извлечении корня n-ой степени из 1 в поле комплексных чисел. Другими словами, будем рассматривать вопрос о решении уравнения zn = 1, где n Î N в поле комплексных чисел. Например, корень квадратный из числа 1 имеет два значения: 1 и – 1. Действительно, 12 = 1 и (– 1)2 = 1. Корень четвертой степени из числа 1 в поле комплексных чисел имеет четыре значения: два действительных, 1 и – 1, и два мнимых, i и – i. Этот факт можно установить проверкой: 14 = 1 и (– 1)4 = 1; i4 = 1 и (– i)4 = 1. Эти два примера наводят на предположение о том, что корень кубический из 1 в поле комплексных чисел должен иметь 3 значения; корень пятой степени из 1 должен иметь пять значений и т.д. Корень n-й степени из числа 1 в поле комплексных чисел должен иметь n значений. Это предположение оказывается верным. Воспользовавшись формулой Муавра, можно доказать, что уравнение zn = 1 в поле комплексных чисел имеет ровно n решений, т. е. корень n-й степени из числа z в поле комплексных чисел имеет ровно n значений. Эти значения корня При помощи формулы Эйлера можно определить функции
Далее можно ввести понятие тригонометрических функций комплексной переменной. Пусть
Известное тождество Эйлера, связывающее пять фундаментальных математических констант:
является частным случаем формулы Эйлера при Благодаря формуле Эйлера появилась так называемая тригонометрическая и показательная запись комплексного числа: Также значительным следствием можно считать формулы возведения комплексного числа в произвольную степень: Формула возведения в степень верна не только для целых
|



 изображаются вершинами правильного n-угольника, вписанного в единичную окружность, причем точка (0; 1) является одной из вершин этого многоугольника.
изображаются вершинами правильного n-угольника, вписанного в единичную окружность, причем точка (0; 1) является одной из вершин этого многоугольника.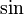 и
и 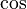 следующим образом:
следующим образом: ,
,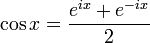 .
.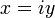 , тогда:
, тогда: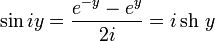 ,
, .
.
 .
.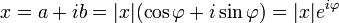 .
.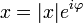 ,
, 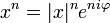 . Геометрический смысл данной формулы следующий: при возведении числа
. Геометрический смысл данной формулы следующий: при возведении числа  в степень
в степень 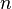 его расстояние до центра возводится в степень
его расстояние до центра возводится в степень 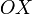 увеличивается в
увеличивается в 


