Кінетична енергія. Теорема про зміну кінетичної енергії.Розглянемо матеріальну точку масою . Знайдемо роботу сили
(при виведенні враховувалось, що Вже згадувалось, що виконувана над тілом робота є мірою зміни його енергії
Прирівняємо праві частини останніх рівностей
Легко переконатись способом підстановки, що дане рівняння задовольняє функція
де Сталу
Таким чином, всяке рухоме тіло має енергію, що виражається формулою (4). Таку енергію, тобто енергію механічного руху називають кінетичною
При переході до системи з
де Провівши в цьому рівнянні сумування по індексу і від 1 до
де Рівняння (1.65) виражає зміст теореми про зміну кінетичної енергії системи: зміна кінетичної енергії системи дорівнює роботі всіх (як зовнішніх, так і внутрішніх) сил прикладених до системи.
|
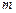, на яку з боку інших тіл діє сила 
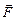. За другим законом Ньютона
).
.
.
,
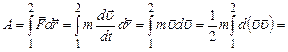
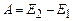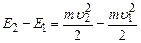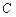– довільна стала величина.
енергія 
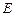була рівною нулю. За такою умовою маємо 
. Звідки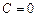 
. Тоді
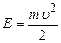. (1.64)
.
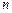взаємодіючих між собою матеріальних точок маємо виділити роботи як зовнішніх, так і внутрішніх сил. Тоді для якоїсь 
тої матеріальної точки будемо мати
,
і 
– відповідно роботи зовнішніх і внутрішніх сил, що діють на 
ту матеріальну точку.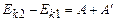
, (1.65)
, 
, 
, 
.
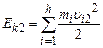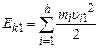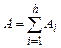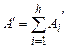