Повертаючись до формул (1.66), (1.67) прирівняємо їх праві частини
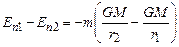 .
.
Це рівняння перетворює в тотожність функція
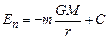 . (1.68)
. (1.68)
Довільну сталу 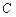 у виразі (1.68) виберемо такою, щоб при
у виразі (1.68) виберемо такою, щоб при  енергія
енергія 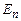 була рівною нулю. За такої умови
була рівною нулю. За такої умови  . Звідки
. Звідки 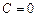 . Отже, потенціальна енергія гравітаційної взаємодії має вираження
. Отже, потенціальна енергія гравітаційної взаємодії має вираження
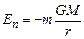 . (1.69)
. (1.69)
Формулу (1.69) застосовують у механіці космічних польотів. В задачах про рух тіл біля Землі користуються наближеним виразом потенціальної енергії.
Для його виведення запишемо (1.68) в дещо іншому вигляді
 ,
,
де  і
і  – відповідно радіус Землі і висота піднімання тіла, також бралось до уваги, що прискорення вільного падіння біля поверхні Землі
– відповідно радіус Землі і висота піднімання тіла, також бралось до уваги, що прискорення вільного падіння біля поверхні Землі  .
.
Біля поверхні Землі 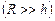
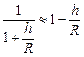 .
.
Тоді
 .
.
Довільну сталу 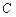 виберемо такою, щоб при
виберемо такою, щоб при 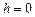 енергія
енергія  . За такої умови
. За такої умови  . Звідки
. Звідки  . Отже, для потенціальної енергії тіла біля поверхні Землі, тобто в однорідному полі сил тяжіння можна користуватись формулою
. Отже, для потенціальної енергії тіла біля поверхні Землі, тобто в однорідному полі сил тяжіння можна користуватись формулою
 .
.

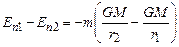 .
.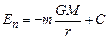 . (1.68)
. (1.68)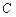 у виразі (1.68) виберемо такою, щоб при
у виразі (1.68) виберемо такою, щоб при  енергія
енергія 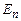 була рівною нулю. За такої умови
була рівною нулю. За такої умови  . Звідки
. Звідки 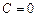 . Отже, потенціальна енергія гравітаційної взаємодії має вираження
. Отже, потенціальна енергія гравітаційної взаємодії має вираження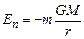 . (1.69)
. (1.69) ,
, і
і  – відповідно радіус Землі і висота піднімання тіла, також бралось до уваги, що прискорення вільного падіння біля поверхні Землі
– відповідно радіус Землі і висота піднімання тіла, також бралось до уваги, що прискорення вільного падіння біля поверхні Землі  .
.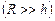
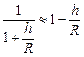 .
. .
.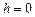 енергія
енергія  . За такої умови
. За такої умови  . Звідки
. Звідки  . Отже, для потенціальної енергії тіла біля поверхні Землі, тобто в однорідному полі сил тяжіння можна користуватись формулою
. Отже, для потенціальної енергії тіла біля поверхні Землі, тобто в однорідному полі сил тяжіння можна користуватись формулою .
.


