Законы теплового излучения
На основании экспериментальных данных Йозеф Стефан (1835-1893) в 1879 году пришел к заключению, что излучательная способность абсолютно черного тела прямо пропорциональна четвертой степени температуры
В 1884 году Людвиг Больцман (1844-1906) вывел это соотношение теоретически. Он использовал выражение, описывающее давление изотропного излучения, вытекающее из электродинамики Максвелла, а также учитывая термодинамические соображения. Постоянная пропорциональности Следующий важный шаг в изучении равновесного излучения сделал Вильгельм Вин (1864-1928) в 1893 году. Рассматривая адиабатическое сжатие равновесного излучения в полости с идеальными зеркальными стенками, и, учитывая изменение частоты при отражении от поверхности движущегося зеркала, Вин показал, что спектральная плотность должна иметь вид
Это соотношение, получившее название закона Вина, сводит задачу нахождения функции двух аргументов w и T к задаче нахождения функции одного аргумента w/ T. Хотя и в законе Вина вид функции I. Длина волны, соответствующая максимуму излучательной способности, обратно пропорциональна абсолютной температуре. Запишем закон Вина для длин волн. Количество энергии в определенном спектральном интервале, конечно, не зависит от выбора шкалы, поэтому w ω и w l связаны друг с другом соотношением
Следовательно,
Чтобы найти максимум этой функции необходимо продифференцировать ее и приравнять к нулю. Тогда,
Решение этого уравнения приводит к результату
Значение константы
II. Максимум спектральной плотности излучения пропорционален пятой степени температуры. Действительно,
III. Если известно распределение энергии излучения при данной температуре T 0, то можно определить аналогичное распределение при любой другой температуре T. Из закона смещения следует, что
Закон Вина (7.3.2) включает в себя, как следствие, закон Стефана-Больцмана. Действительно,
Введя новую переменную
Необходимо также отметить, что закон Вина справедлив при больших частотах и низких температурах. Законы Стефана-Больцмана и Вина не дают полного понимания о распределении энергии излучения черного тела. Общий метод теоретического определения функции
где
Соотношение (7.3.8) называют формулой Рэлея-Джинса. Она согласуется с формулой Вина. Действительно, соотношение (7.3.8) можно переписать в виде
Равенство излучательной способности бесконечной величине означает, что равновесие между телом и его излучением установится только при температуре, равной абсолютному нулю. Этот вывод противоречит опыту, так как тела находятся в равновесии с излучением при произвольной, отличной от нуля температуре. Данное несоответствие было названо ультрафиолетовой катастрофой. Причиной ультрафиолетовой катастрофы явилось то, что излучение в полости имеет бесконечное число степеней свободы. Тогда как вещество всегда имеет конечное число степеней свободы. Формула Планка В 1900 году Макс Планк (1858-1947) получил формулу для функции
Для определения среднего значения e n = e0× n, (7.4.2) где n = 1, 2, 3, ¼ после математических преобразований выражения (7.4.1) с учетом условия (7.4.2), получим
Подставляя полученное значение средней энергии осциллятора в формулу (7.3.7), получим
Чтобы это соотношение не противоречило формуле Вина (7.3.2), необходимо принять
Формула (7.4.3) получила название формулы Планка. Сам Планк пользовался не постоянной ħ;, а постоянной Формула Планка хорошо согласуется с экспериментом при всех частотах и температурах. Для малых частот и высоких температур
после чего она принимает вид формулы Рэлея-Джинса
В другом предельном случае (при
Такой вид
Между этими предельными случаями лежит область, в которой находится максимум кривой спектрального распределения.
|

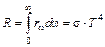 . (7.3.1)
. (7.3.1) получила название постоянной Стефана-Больцмана, а выражение (7.3.1) – законом Стефана-Больцмана.
получила название постоянной Стефана-Больцмана, а выражение (7.3.1) – законом Стефана-Больцмана.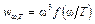 . (7.3.2)
. (7.3.2)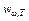 далеко не явный, но из него вытекают некоторые следствия.
далеко не явный, но из него вытекают некоторые следствия.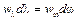 . Диапазоны длин волн d l и частот d w определяются функциональной зависимостью
. Диапазоны длин волн d l и частот d w определяются функциональной зависимостью  , из которой следует
, из которой следует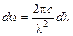 .
.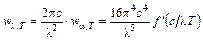 . (7.3.3)
. (7.3.3)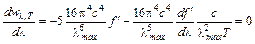 или
или 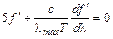 .
.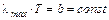 . (7.3.4)
. (7.3.4) было определено из опытных данных. Соотношение (7.3.4) получило название закона смещения.
было определено из опытных данных. Соотношение (7.3.4) получило название закона смещения. Измеряя распределение по длинам волн интенсивности излучения из отверстия в полости, Отто Люммер (1860-1925) и Эрнст Прингсгейм (1859–1917) экспериментально показали, что при некотором значении длины волны lmax кривая
Измеряя распределение по длинам волн интенсивности излучения из отверстия в полости, Отто Люммер (1860-1925) и Эрнст Прингсгейм (1859–1917) экспериментально показали, что при некотором значении длины волны lmax кривая  имеет ярко выраженный максимум. С увеличением температуры максимум смещается в сторону более коротких волн. Экспериментальная проверка, предпринятая Люммером и Прингсгеймом, показала, что формула Вина соответствует действительности лишь в области коротких волн и совершенно неверна для более длинных волн.
имеет ярко выраженный максимум. С увеличением температуры максимум смещается в сторону более коротких волн. Экспериментальная проверка, предпринятая Люммером и Прингсгеймом, показала, что формула Вина соответствует действительности лишь в области коротких волн и совершенно неверна для более длинных волн.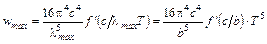 . (7.3.5)
. (7.3.5) . Тогда
. Тогда . (7.3.6)
. (7.3.6) .
.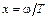 , получим
, получим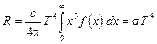 .
.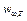 был предложен Джоном Рэлеем (1842-1919) и развит Джеймсом Джинсом (1877-1946). Рэлей и Джинс применили к равновесному излучению в полости теорему классической статистической механики о равномерном распределении кинетической энергии по степеням свободы. Согласно этой теореме, в состоянии статистического равновесия на каждую степень свободы приходится в среднем кинетическая энергия, равная
был предложен Джоном Рэлеем (1842-1919) и развит Джеймсом Джинсом (1877-1946). Рэлей и Джинс применили к равновесному излучению в полости теорему классической статистической механики о равномерном распределении кинетической энергии по степеням свободы. Согласно этой теореме, в состоянии статистического равновесия на каждую степень свободы приходится в среднем кинетическая энергия, равная 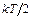 ,где k – постоянная Больцмана. Если степень свободы колебательная, то надо учесть потенциальную энергию. В случае гармонических колебаний, она также равна
,где k – постоянная Больцмана. Если степень свободы колебательная, то надо учесть потенциальную энергию. В случае гармонических колебаний, она также равна  . Эта теорема сводит задачу нахождения
. Эта теорема сводит задачу нахождения 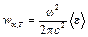 , (7.3.7)
, (7.3.7)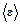 – средняя энергия осциллятора. Тогда,
– средняя энергия осциллятора. Тогда, . (7.3.8)
. (7.3.8) .
. В длинноволновой области, то есть при маленьких w, формула Рэлея-Джинса хорошо согласуется с экспериментом. Но при увеличении w обнаруживается резкое расхождение с экспериментом. Действительно,
В длинноволновой области, то есть при маленьких w, формула Рэлея-Джинса хорошо согласуется с экспериментом. Но при увеличении w обнаруживается резкое расхождение с экспериментом. Действительно, .
. . Однако, поскольку энергия принимает не любое значение, то при вычислении средних значений энергии осциллятора
. Однако, поскольку энергия принимает не любое значение, то при вычислении средних значений энергии осциллятора  интегралы необходимо заменить суммами
интегралы необходимо заменить суммами . (7.4.1)
. (7.4.1) .
.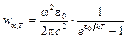 .
.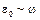 или
или  , где ħ; – постоянная, названная постоянной Планка. В результате, выражение для спектральной плотности равновесного излучения примет вид
, где ħ; – постоянная, названная постоянной Планка. В результате, выражение для спектральной плотности равновесного излучения примет вид . (7.4.3)
. (7.4.3)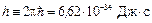 .
.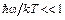 . Тогда экспоненту в формуле Планка можно разложить в ряд
. Тогда экспоненту в формуле Планка можно разложить в ряд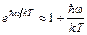 ,
, .
. ) экспонента в знаменателе много больше единицы. Следовательно, формула Планка принимает вид
) экспонента в знаменателе много больше единицы. Следовательно, формула Планка принимает вид .
.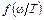 , входящей в формулу (7.3.2)
, входящей в формулу (7.3.2) .
.


