Пусть машины  и
и 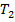 имеют соответственно программы
имеют соответственно программы 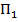 и
и 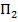 . Предположим, что внутренние алфавиты этих машин не пересекаются и что
. Предположим, что внутренние алфавиты этих машин не пересекаются и что 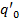 — некоторое заключительное состояние машины
— некоторое заключительное состояние машины  , a
, a 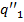 — какое-либо начальное состояние машины
— какое-либо начальное состояние машины 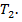 Заменим всюду в программе
Заменим всюду в программе  состояние
состояние 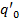 на состояние
на состояние 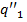 и полученную программу объединим с программой
и полученную программу объединим с программой 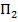 . Новая программа П определяет машину T, называемую композицией машин
. Новая программа П определяет машину T, называемую композицией машин  и
и 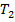 (по паре состояний
(по паре состояний  ) и обозначаемую через
) и обозначаемую через 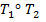 или
или 
 более подробно:
более подробно:  - Внешний алфавит композиции
- Внешний алфавит композиции  является объединением внешних алфавитов машин
является объединением внешних алфавитов машин  и
и 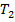 .
.
Пусть q' — некоторое заключительное состояние машины Г, а q"; — какое-либо состояние машины T, не являющееся заключительным. Заменим всюду в программе П машины T символ q' на q". Получим программу П ', определяющую машину T'(q', q"). Машина T' называется итерацией машины T (по паре состояний 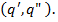
Пусть машины Тьюринга  ,
, 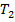 и
и 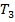 задаются программами
задаются программами 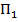 ,
, 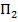 и
и 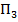 соответственно. Считаем, что внутренние алфавиты этих машин попарно не пересекаются. Пусть
соответственно. Считаем, что внутренние алфавиты этих машин попарно не пересекаются. Пусть 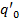 и
и  — какие-либо различные заключительные состояния машины
— какие-либо различные заключительные состояния машины  . Заменим всюду в программе
. Заменим всюду в программе 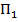 состояние
состояние 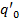 некоторым начальным состоянием
некоторым начальным состоянием  машины
машины 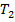 , а состояние
, а состояние  некоторым начальным состоянием
некоторым начальным состоянием 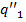 машины
машины 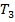 . Затем новую программу объединим с программами
. Затем новую программу объединим с программами 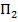 и
и 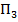 . Получим программу П, задающую машину Тьюринга
. Получим программу П, задающую машину Тьюринга  . Эта машина называется разветвлением машин
. Эта машина называется разветвлением машин 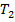 и
и 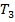 , управляемым машиной
, управляемым машиной  .
.
При задании сложных машин Тьюринга часто применяют так называемую операторную запись алгоритма, которая представляет собой строку, состоящую из символов, обозначающих машины, символов перехода (вида  и
и  ), а также символов α и ω;, служащих для обозначения соответственно начала и окончания работы алгоритма. В операторной записи (некоторого алгоритма) выражение
), а также символов α и ω;, служащих для обозначения соответственно начала и окончания работы алгоритма. В операторной записи (некоторого алгоритма) выражение 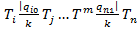 ,обозначает разветвление машин
,обозначает разветвление машин 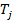 и
и 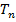 , управляемое машиной
, управляемое машиной 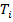 , причем заключительное состояние
, причем заключительное состояние  машины
машины 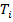 заменяется начальным состоянием
заменяется начальным состоянием 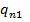 машины
машины 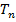 , а всякое другое заключительное состояние машины
, а всякое другое заключительное состояние машины 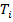 заменяется начальным состоянием машины
заменяется начальным состоянием машины 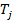 (одним и тем же). Если машина
(одним и тем же). Если машина 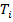 имеет одно заключительное состояние, то символы
имеет одно заключительное состояние, то символы 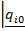 и
и 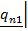 служат для обозначения безусловного перехода. Там, где не могут возникнуть недоразумения, символы
служат для обозначения безусловного перехода. Там, где не могут возникнуть недоразумения, символы  и
и 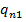 опускаются.
опускаются.
Пример 3. Операторная схема

описывает следующий «процесс вычисления». Начинает работу машина 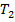 . Если она заканчивает работу в состоянии
. Если она заканчивает работу в состоянии 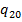 , то начинает работать машина
, то начинает работать машина  , а по окончании работы машины
, а по окончании работы машины  вновь «выполняет работу» машина
вновь «выполняет работу» машина 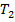 . Если же машина
. Если же машина 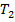 останавливается в некотором заключительном состоянии, отличном от
останавливается в некотором заключительном состоянии, отличном от  то «работу продолжает» машина
то «работу продолжает» машина  Если
Если 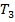 приходит в заключительное состояние
приходит в заключительное состояние  , то начинает работу машина
, то начинает работу машина  ; если же
; если же 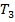 заканчивает работу в некотором заключительном состоянии, отличном от
заканчивает работу в некотором заключительном состоянии, отличном от  , то «работу продолжает» машина
, то «работу продолжает» машина 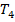 . Если машина
. Если машина 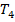 когда-либо остановится, то процесс вычисления на этом заканчивается.
когда-либо остановится, то процесс вычисления на этом заканчивается.

 и
и 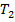 имеют соответственно программы
имеют соответственно программы 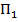 и
и 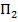 . Предположим, что внутренние алфавиты этих машин не пересекаются и что
. Предположим, что внутренние алфавиты этих машин не пересекаются и что 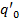 — некоторое заключительное состояние машины
— некоторое заключительное состояние машины 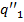 — какое-либо начальное состояние машины
— какое-либо начальное состояние машины 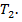 Заменим всюду в программе
Заменим всюду в программе  состояние
состояние 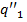 и полученную программу объединим с программой
и полученную программу объединим с программой  ) и обозначаемую через
) и обозначаемую через 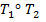 или
или 
 более подробно:
более подробно:  - Внешний алфавит композиции
- Внешний алфавит композиции 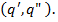
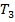 задаются программами
задаются программами 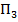 соответственно. Считаем, что внутренние алфавиты этих машин попарно не пересекаются. Пусть
соответственно. Считаем, что внутренние алфавиты этих машин попарно не пересекаются. Пусть  — какие-либо различные заключительные состояния машины
— какие-либо различные заключительные состояния машины  машины
машины 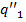 машины
машины  . Эта машина называется разветвлением машин
. Эта машина называется разветвлением машин  и
и  ), а также символов α и ω;, служащих для обозначения соответственно начала и окончания работы алгоритма. В операторной записи (некоторого алгоритма) выражение
), а также символов α и ω;, служащих для обозначения соответственно начала и окончания работы алгоритма. В операторной записи (некоторого алгоритма) выражение 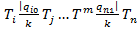 ,обозначает разветвление машин
,обозначает разветвление машин 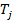 и
и 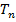 , управляемое машиной
, управляемое машиной 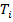 , причем заключительное состояние
, причем заключительное состояние  машины
машины 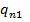 машины
машины 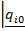 и
и 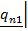 служат для обозначения безусловного перехода. Там, где не могут возникнуть недоразумения, символы
служат для обозначения безусловного перехода. Там, где не могут возникнуть недоразумения, символы 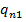 опускаются.
опускаются.
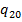 , то начинает работать машина
, то начинает работать машина  то «работу продолжает» машина
то «работу продолжает» машина  Если
Если  , то начинает работу машина
, то начинает работу машина  , то «работу продолжает» машина
, то «работу продолжает» машина 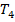 . Если машина
. Если машина 


