Предложение 15. 2 Однородная система уравнений 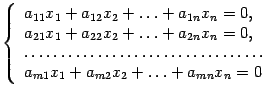 (15.7) всегда является совместной. Доказательство. Для этой системы набор чисел
(15.7) всегда является совместной. Доказательство. Для этой системы набор чисел 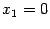 ,
, 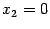 ,
,  ,
,  является решением. В этом разделе мы будем использовать матричную запись системы:
является решением. В этом разделе мы будем использовать матричную запись системы: 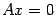 . Предложение 15. 3 Сумма решений однородной системы линейных уравнений является решением этой системы. Решение, умноженное на число, тоже является решением. Доказательство. Пусть
. Предложение 15. 3 Сумма решений однородной системы линейных уравнений является решением этой системы. Решение, умноженное на число, тоже является решением. Доказательство. Пусть 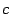 и
и 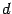 служат решениями системы
служат решениями системы 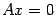 . Тогда
. Тогда  и
и 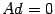 . Пусть
. Пусть 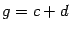 . Тогда
. Тогда 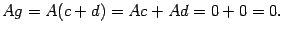 Так как
Так как  , то
, то 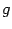 -- решение. Пусть
-- решение. Пусть 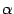 -- произвольное число,
-- произвольное число,  . Тогда
. Тогда  Так как
Так как 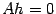 , то
, то  -- решение. Следствие 15. 1 Если однородная система линейных уравнений имеет ненулевое решение, то она имеет бесконечно много различных решений. Действительно, умножая ненулевое решение на различные числа, будем получать различные решения. Определение 15. 5 Будем говорить, что решения
-- решение. Следствие 15. 1 Если однородная система линейных уравнений имеет ненулевое решение, то она имеет бесконечно много различных решений. Действительно, умножая ненулевое решение на различные числа, будем получать различные решения. Определение 15. 5 Будем говорить, что решения  системы
системы 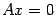 образуют фундаментальную систему решений, если столбцы
образуют фундаментальную систему решений, если столбцы  образуют линейно независимую систему и любое решение системы является линейной комбинацией этих столбцов. Определение 15. 6 Пусть
образуют линейно независимую систему и любое решение системы является линейной комбинацией этих столбцов. Определение 15. 6 Пусть  -- фундаментальная система решений однородной системы
-- фундаментальная система решений однородной системы 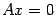 . Тогда выражение
. Тогда выражение 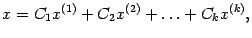 где
где  -- произвольные числа, будем называть общим решением системы
-- произвольные числа, будем называть общим решением системы 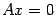 . Из определения фундаментальной системы решений следует, что любое решение однородной системы может быть получено из общего решения при некоторых значениях
. Из определения фундаментальной системы решений следует, что любое решение однородной системы может быть получено из общего решения при некоторых значениях  . И наоборот, при любых фиксированных числовых значениях
. И наоборот, при любых фиксированных числовых значениях  из общего решения получим решение однородной системы. Как находить фундаментальную систему решений мы увидим позже, в разделе "Алгоритм нахождения решений произвольной системы линейных уравнений (метод Гаусса)". Теорема 15. 3 Пусть
из общего решения получим решение однородной системы. Как находить фундаментальную систему решений мы увидим позже, в разделе "Алгоритм нахождения решений произвольной системы линейных уравнений (метод Гаусса)". Теорема 15. 3 Пусть  -- фундаментальная система решений однородной системы
-- фундаментальная система решений однородной системы 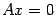 . Тогда
. Тогда  , где
, где 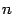 -- число неизвестных в системе. Доказательство читатель может найти, например, в [1].
-- число неизвестных в системе. Доказательство читатель может найти, например, в [1].