Вектор 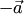 называется противоположным вектору
называется противоположным вектору 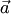 , если их сумма равна нулевому вектору:
, если их сумма равна нулевому вектору: 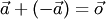 . Противоположный вектор имеет длину
. Противоположный вектор имеет длину 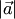 , коллинеарен и противоположно направлен вектору
, коллинеарен и противоположно направлен вектору 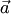 (рис.1.8,а,б). Нулевой вектор является противоположным самому себе.
(рис.1.8,а,б). Нулевой вектор является противоположным самому себе.
Разностью векторов 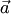 и
и  называется сумма вектора
называется сумма вектора 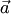 с вектором
с вектором 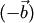 , противоположным вектору
, противоположным вектору  :
:

Для нахождения разности векторов 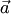 и
и  приложим к произвольной точке
приложим к произвольной точке 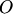 векторы
векторы  , а также вектор
, а также вектор  , противоположный вектору
, противоположный вектору  (рис.1.9,а). Искомую разность находим по правилу параллелограмма:
(рис.1.9,а). Искомую разность находим по правилу параллелограмма:
Для нахождения разности проще использовать правило треугольника (рис. 1.9,6). Для этого прикладываем к произвольной точке 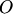 векторы
векторы  . Вектор
. Вектор  при этом равен искомой разности
при этом равен искомой разности  .
.
Вычитание векторов — действие, обратное сложению — можно определить также следующим образом: разностью векторов 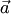 и
и  называется такой вектор
называется такой вектор  , который в сумме с вектором
, который в сумме с вектором  дает вектор
дает вектор 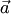 (рис.1.9,в), т.е. разность
(рис.1.9,в), т.е. разность 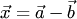 — это решение уравнения
— это решение уравнения  .
.

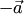 называется противоположным вектору
называется противоположным вектору 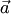 , если их сумма равна нулевому вектору:
, если их сумма равна нулевому вектору: 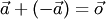 . Противоположный вектор имеет длину
. Противоположный вектор имеет длину 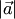 , коллинеарен и противоположно направлен вектору
, коллинеарен и противоположно направлен вектору  называется сумма вектора
называется сумма вектора 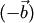 , противоположным вектору
, противоположным вектору 
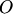 векторы
векторы  , а также вектор
, а также вектор  , противоположный вектору
, противоположный вектору  при этом равен искомой разности
при этом равен искомой разности  .
. , который в сумме с вектором
, который в сумме с вектором 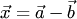 — это решение уравнения
— это решение уравнения  .
.


