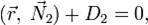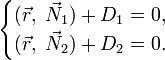Уравнения прямой в пространстве
Векторное параметрическое уравнение прямой в пространстве: где
Параметрическое уравнение прямой в пространстве:
где Каноническое уравнение прямой в пространстве:
Общее векторное уравнение прямой в пространстве: Поскольку прямая является пересечением двух различных непараллельных плоскостей, заданных соответственно общими уравнениями: и то уравнение прямой можно задать системой этих уравнений:
|
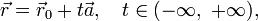
— радиус-вектор некоторой фиксированной точки M0, лежащей на прямой, 
— ненулевой вектор, коллинеарный этой прямой,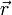 
— радиус-вектор произвольной точки прямой.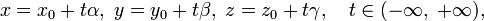
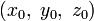— координаты некоторой фиксированной точки M0, лежащей на прямой; 
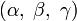— координаты вектора, коллинеарного этой прямой.
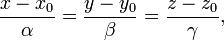где 
