Теорема. (Необходимое и достаточное условие линейной зависимости системы векторов.)
Система векторов векторного пространства является линейно зависимой тогда и только тогда, когда один из векторов системы линейно выражается через другие вектора этой системы.
Доказательство. Необходимость. Пустьсистема
Разделим обе части предыдущего равенства на этот ненулевой коэффициент (т.е. умножим на
Тогда Достаточность. Пусть один из векторов системы линейно выражается через другие вектора этой системы:
.Перенесем вектор Так как коэффициент при векторе
|
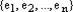линейно зависимая. Тогда, по определению, она представляет нулевой вектор нетривиально, т.е. существует нетривиальная линейная комбинация данной системы векторов равная нулевому вектору: 
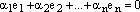, где хотя бы один из коэффициентов этой линейной комбинации не равен нулю. Пусть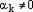 
: 
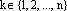
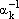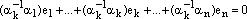Обозначим: 
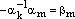, где 
.
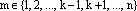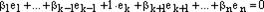или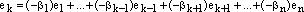 
,т.е. один из векторов системы линейно выражается через другие векторы этой системы, ч.т.д.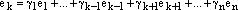
в правую часть этого равенства: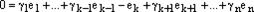 
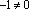, то мы имеем нетривиальное представление нуля системой векторов 
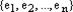, что означает, что эта система векторов является линейно зависимой, ч.т.д.Теорема доказана.
