Евклидовы пространства.Определение 1. Линейное пространство E = {f, g, h, …} называется евклидовым, если ставится в соответствие число, называемое скалярным произведением:.
Наглядными примерами евклидовых пространств могут служить пространства:
Евклидово пространство можно считать современной интерпретацией и обобщением (так как оно допускает размерности больше трех) классической (Евклидовой) геометрии.
Более абстрактный пример: пространство вещественных многочленов p(x) степени, не превосходящей n, со скалярным произведением, определенным как интеграл произведения по конечному отрезку (или по всей прямой, но с быстро спадающей весовой функцией, например
|
При этом, для 
выполняются аксиомы: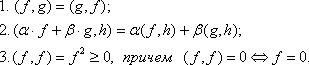
размерности 1 (вещественная прямая)
размерности 2 (евклидова плоскость)
размерности 3 (евклидово трехмерное пространство)
)
