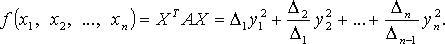Критерий Сильвестра
Квадратичная форма является положительно определенной, тогда и только тогда, когда все угловые миноры её матрицы строго положительны. Квадратичная форма является отрицательно определенной, тогда и только тогда, когда знаки всех угловых миноров её матрицы чередуются, причем минор порядка 1 отрицателен. Билинейная форма, полярная положительно определённой квадратичной форме, удовлетворяет всем аксиомам скалярного произведения. Для любой квадратичной формы существует базис, в котором её матрица диагональна, а сама форма имеет канонический вид:
Разность между числом положительных (p) и отрицательных (n − p) членов в этой записи называется сигнатурой квадратичной формы. Сигнатура, также как и числа положительных и отрицательных слагаемых, не зависят от способов приведения квадратичной формы к каноническому виду (закон инерции Сильвестра). Для приведения квадратичной формы к каноническому виду обычно используется метод Лагранжа. Канонический вид квадратичной формы Квадратичная форма называется канонической, если все
Всякую квадратичную форму можно привести к каноническому виду с помощью линейных преобразований. На практике обычно применяют следующие способы. 1. Ортогональное преобразование пространства
где 2. Метод Лагранжа - последовательное выделение полных квадратов. Например, если Затем подобную процедуру проделывают с квадратичной формой
3. Метод Якоби (в случае, когда все главные миноры
|


 т. е.
т. е.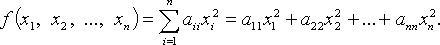
 :
: 
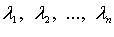 - собственные значения матрицы A.
- собственные значения матрицы A.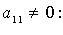
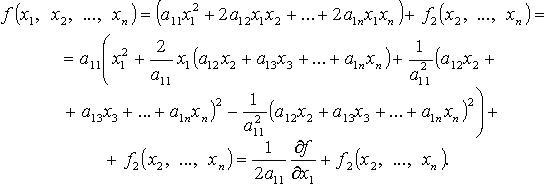
 и т. д. Если в квадратичной форме все
и т. д. Если в квадратичной форме все 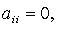 но есть
но есть  то после предварительного преобразования дело сводится к р ассмотренной процедуре. Так, если, например,
то после предварительного преобразования дело сводится к р ассмотренной процедуре. Так, если, например,  то полагаем
то полагаем 
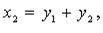
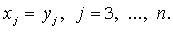
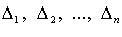 квадратичной формы отличны от нуля):
квадратичной формы отличны от нуля):