Взаимное расположение нескольких прямых на плоскости
Две прямые, заданные уравнениями или пересекаются в точке Угол γ12 между пересекающимися прямыми определяется формулой
При этом под γ12 понимается угол, на который надо повернуть первую прямую (заданную параметрами A1, B1, C1, k1 и b1) вокруг точки пересечения против часовой стрелки до первого совмещения со второй прямой.
Эти прямые параллельны, если A1B2 − A2B1 = 0 или k1 = k2, и перпендикулярны, если A1A2 + B1B2 = 0 или
Любую прямую, параллельную A1x + B1y + C1 = 0, можно выразить уравнением A1x + B1y + C = 0. При этом расстояние между ними будет равно
Если знак перед радикалом противоположен C1, то δ будет положительным, когда вторая прямая и начало координат лежат по разные стороны от первой прямой. Для того, чтобы три прямые пересекались в одной точке или были параллельны друг другу, необходимо и достаточно, чтобы выполнялось условие
Если
20. Углом между прямыми в пространстве будем называть любой из смежных углов, образованных двумя прямыми, проведёнными через произвольную точку параллельно данным.
Пусть в пространстве заданы две прямые:
Очевидно, что за угол φ между прямыми можно принять угол между их направляющими векторами
Две прямые параллельны тогда и только тогда, когда их соответствующие коэффициенты пропорциональны, т.е. l1 параллельна l2 тогда и только тогда, когда s1 параллелен.
Две прямые перпендикулярны тогда и только тогда, когда сумма произведений соответствующих коэффициентов равна нулю:.
Углом между прямой и плоскостью будем называть угол, образованный прямой и её проекцией наплоскость. Пусть прямаяи плоскость заданы уравнениями
Рассмотрим векторы
Если угол между векторами
Условие перпендикулярности прямой и плоскости. Прямая и плоскость перпендикулярны тогда и только тогда, когда направляющий вектор прямой Условие параллельности прямой и плоскости. Прямая и плоскость параллельны тогда и только тогда, когда векторы 21. Линейное, или векторное пространство 1.сложения, то есть каждой паре элементов множества 2.умножения на скаляр (то есть элемент поля P), то есть любому элементу
При этом на операции накладываются следующие условия: 1. 2. 3.существует такой элемент 4.для любого 5. 6. 7. 8.
Элементы множества L называют векторами, а элементы поля P — скалярами. Свойства 1-4 совпадают с аксиомами абелевой группы.
|


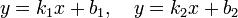

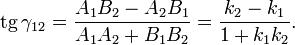
 .
.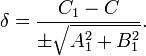
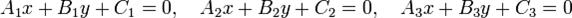

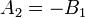 и
и  , то прямые
, то прямые  и
и  перпендикулярны.
перпендикулярны.
 и
и  . Так как
. Так как  , то по формуле для косинуса угла между векторами получим
, то по формуле для косинуса угла между векторами получим 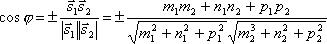 Условия параллельности и перпендикулярности двух прямых равносильны условиям параллельности и перпендикулярности их направляющих векторов S1 и
Условия параллельности и перпендикулярности двух прямых равносильны условиям параллельности и перпендикулярности их направляющих векторов S1 и 


 и
и  . Если угол между ними острый, то он будет
. Если угол между ними острый, то он будет  , где φ – угол между прямой и плоскостью. Тогда
, где φ – угол между прямой и плоскостью. Тогда  .
. и
и  . Следовательно
. Следовательно 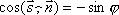 . Поэтому в любом случае
. Поэтому в любом случае  . Вспомнив формулу вычисления косинуса угла между векторами, получим.
. Вспомнив формулу вычисления косинуса угла между векторами, получим.
 ..
..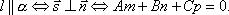
 над полем P — это непустое множество L, на котором введены операции
над полем P — это непустое множество L, на котором введены операции ставится в соответствие элемент того же множества, обозначаемый
ставится в соответствие элемент того же множества, обозначаемый 
 и любому элементу
и любому элементу  ставится в соответствие единственный элемент из
ставится в соответствие единственный элемент из  .
. ., для любых
., для любых  , для любых
, для любых  (ассоциативность сложения);
(ассоциативность сложения); , что д
, что д  для любого
для любого  , что
, что  (существование противоположного элемента относительно сложения).
(существование противоположного элемента относительно сложения). (ассоциативность умножения на скаляр);
(ассоциативность умножения на скаляр); (унитарность: умножение на нейтральный (по умножению) элемент поля P сохраняет вектор).
(унитарность: умножение на нейтральный (по умножению) элемент поля P сохраняет вектор).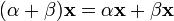 (дистрибутивность умножения на вектор относительно сложения скаляров);
(дистрибутивность умножения на вектор относительно сложения скаляров); (дистрибутивность умножения на скаляр относительно сложения векторов).
(дистрибутивность умножения на скаляр относительно сложения векторов).


