Произведением ненулевого вектора а на действительное число 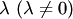 называется вектор
называется вектор  , удовлетворяющий условиям:
, удовлетворяющий условиям:
1) длина вектора  равна
равна 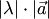 , т.е.
, т.е. 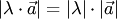 ;
;
2) векторы  и
и 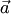 коллинеарные
коллинеарные  ;
;
3) векторы  и
и 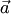 одинаково направлены, если
одинаково направлены, если 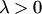 , и противоположно направлены, если
, и противоположно направлены, если 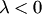 .
.
Произведение нулевого вектора на любое число  считается (по определению) нулевым вектором:
считается (по определению) нулевым вектором:  ; произведение любого вектора на число нуль также считается нулевым вектором:
; произведение любого вектора на число нуль также считается нулевым вектором: 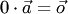 . Из определения произведения следует, что:
. Из определения произведения следует, что:
а) при умножении на единицу  вектор не изменяется:
вектор не изменяется: 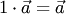 ;
;
б) при умножении вектора на 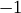 получается противоположный вектор:
получается противоположный вектор:  ;
;
в) деление вектора на отличное от нуля число  сводится к его умножению на число
сводится к его умножению на число  , обратное
, обратное  .
.
г) при делении ненулевого вектора 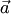 на его длину, т.е. при умножении
на его длину, т.е. при умножении 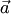 на число
на число  получаем единичный вектор, одинаково направленный с вектором
получаем единичный вектор, одинаково направленный с вектором 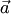 .
.
Действительно, длина вектора 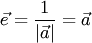 равна единице:
равна единице: 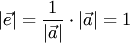 .
.
Вектор 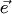 коллинеарен и одинаково направлен с вектором
коллинеарен и одинаково направлен с вектором 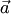 , так как
, так как  ;
;
д) при умножении единичного вектора на число  получаем коллинеарный ему вектор, длина которого равна
получаем коллинеарный ему вектор, длина которого равна 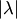 .
.
На рис.1.10 изображены векторы, получающиеся в результате умножения данного вектора 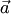 на
на 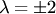 и
и 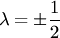 , а также противоположный вектор
, а также противоположный вектор  .
.

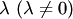 называется вектор
называется вектор  , удовлетворяющий условиям:
, удовлетворяющий условиям: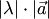 , т.е.
, т.е. 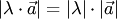 ;
;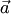 коллинеарные
коллинеарные  ;
;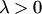 , и противоположно направлены, если
, и противоположно направлены, если 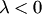 .
. считается (по определению) нулевым вектором:
считается (по определению) нулевым вектором:  ; произведение любого вектора на число нуль также считается нулевым вектором:
; произведение любого вектора на число нуль также считается нулевым вектором: 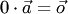 . Из определения произведения следует, что:
. Из определения произведения следует, что: вектор не изменяется:
вектор не изменяется: 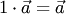 ;
;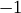 получается противоположный вектор:
получается противоположный вектор:  ;
; сводится к его умножению на число
сводится к его умножению на число  , обратное
, обратное  .
. получаем единичный вектор, одинаково направленный с вектором
получаем единичный вектор, одинаково направленный с вектором 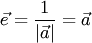 равна единице:
равна единице: 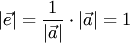 .
.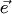 коллинеарен и одинаково направлен с вектором
коллинеарен и одинаково направлен с вектором  ;
;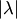 .
.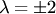 и
и 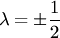 , а также противоположный вектор
, а также противоположный вектор  .
.


