Пусть даны два вектора 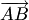 и
и 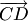 . Приложим вектор
. Приложим вектор 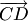 к точке
к точке  (концу вектора
(концу вектора 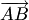 ) и получим вектор
) и получим вектор 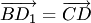 (рис.1.7,а; здесь и далее равные векторы отмечены одинаковыми засечками). Вектор
(рис.1.7,а; здесь и далее равные векторы отмечены одинаковыми засечками). Вектор  называется суммой векторов
называется суммой векторов 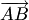 и
и 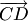 и обозначается
и обозначается 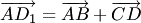 . Это нахождение суммы называется правилом треугольника.
. Это нахождение суммы называется правилом треугольника.
Сумму двух неколлинеарных векторов 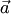 и
и  можно найти по правилу параллелограмма. Для этого откладываем от любой точки
можно найти по правилу параллелограмма. Для этого откладываем от любой точки 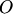 векторы
векторы 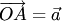 и
и 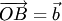 , а затем строим параллелограмм
, а затем строим параллелограмм 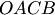 (рис. 1.7,6). Диагональ
(рис. 1.7,6). Диагональ 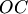 параллелограмма определяет сумму:
параллелограмма определяет сумму: 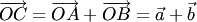 .
.
Для нахождения суммы нескольких векторов можно построить ломаную из равных им векторов. Тогда замыкающий вектор, соединяющий начало первого вектора ломаной с концом последнего ее вектора, равен сумме всех векторов ломаной. На рис.1.7,в изображена сумма 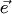 четырех векторов
четырех векторов  . Таким способом (правило ломаной) можно сложить любое конечное число векторов. Заметим, что сумма векторов не зависит от точек приложения слагаемых и от порядка суммирования. Например, "выстраивая цепочку" векторов для суммы в виде
. Таким способом (правило ломаной) можно сложить любое конечное число векторов. Заметим, что сумма векторов не зависит от точек приложения слагаемых и от порядка суммирования. Например, "выстраивая цепочку" векторов для суммы в виде 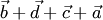 , получим вектор, равный вектору
, получим вектор, равный вектору 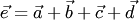 . Если ломаная получилась замкнутой, то сумма равна нулевому вектору.
. Если ломаная получилась замкнутой, то сумма равна нулевому вектору.

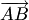 и
и 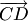 . Приложим вектор
. Приложим вектор  (концу вектора
(концу вектора 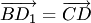 (рис.1.7,а; здесь и далее равные векторы отмечены одинаковыми засечками). Вектор
(рис.1.7,а; здесь и далее равные векторы отмечены одинаковыми засечками). Вектор  называется суммой векторов
называется суммой векторов 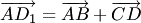 . Это нахождение суммы называется правилом треугольника.
. Это нахождение суммы называется правилом треугольника.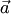 и
и  можно найти по правилу параллелограмма. Для этого откладываем от любой точки
можно найти по правилу параллелограмма. Для этого откладываем от любой точки 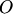 векторы
векторы 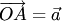 и
и 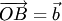 , а затем строим параллелограмм
, а затем строим параллелограмм 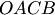 (рис. 1.7,6). Диагональ
(рис. 1.7,6). Диагональ 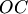 параллелограмма определяет сумму:
параллелограмма определяет сумму: 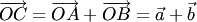 .
.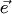 четырех векторов
четырех векторов  . Таким способом (правило ломаной) можно сложить любое конечное число векторов. Заметим, что сумма векторов не зависит от точек приложения слагаемых и от порядка суммирования. Например, "выстраивая цепочку" векторов для суммы в виде
. Таким способом (правило ломаной) можно сложить любое конечное число векторов. Заметим, что сумма векторов не зависит от точек приложения слагаемых и от порядка суммирования. Например, "выстраивая цепочку" векторов для суммы в виде 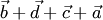 , получим вектор, равный вектору
, получим вектор, равный вектору 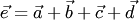 . Если ломаная получилась замкнутой, то сумма равна нулевому вектору.
. Если ломаная получилась замкнутой, то сумма равна нулевому вектору.


