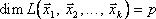Определение. Число векторов в базисе векторного пространства называется его размерностью.
Обозначение: Таким образом, в соответствие с этим и предыдущими определениями, имеем:
1)
2)
3)
Замечание. Если Таким образом, любой вектор прямой L, плоскости Р и пространства S можно разложить по базису
.Обозначение. В силу теоремы о равенстве векторов, мы можем отождествить любой вектор с упорядоченной тройкой действительных чисел и писать:
. Это возможно лишь том случае, когда базис Определение. Запись вектора в виде упорядоченной тройки действительных чисел называют координатной формой записи вектора: Определение. Пусть V и W – произвольные векторные пространства над полем К. Гомоморфизм 24. Непустое множество 1. 2. Пусть UиW — подпространства векторного пространства V над полемF. Предложение 1. Пересечение Замечание 1. Объединение Определение 1. Суммой1) подпространств W иU называется наименьшее подпространство в V, содержащее UиW, то есть
. Вообще говоря, можно определить сумму любого конечного числа подпространств: Определение 1'. Сумма подпространств
. Предложение 2. Пусть U иW — подпространства конечномерного векторного пространства V. Тогда Прямой суммой векторных пространств U иW называется декартово произведение . 25. Линейной оболочкой заданной конечной совокупности . Линейные оболочки обладают следующими свойствами: 1. Линейная оболочка элементов векторного пространства Rn является подпространством М векторного пространства Rn.Данный результат следует из определения линейной оболочки: сумма двух векторов из линейной оболочки будет принадлежать линейной оболочки (одна из линейных комбинаций), произведение вектора из линейной оболочки также будет принадлежать линейной оболочки. 2. Линейная оболочка может совпадать со всем пространством Rn (если образующая система является базисом в пространстве Rn) 3. Линейная оболочка 4. Если какой-нибудь элемент из порождающей системы элементов 5. Если координатная матрица системы образующих
|

 – размерность векторного пространства V.
– размерность векторного пространства V.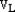 – векторное пространство векторов прямой L.
– векторное пространство векторов прямой L.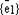 – базис
– базис 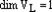 ,
, 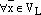 ,
,  – разложение вектора
– разложение вектора 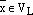 по базису
по базису 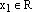 – координата вектора
– координата вектора  относительно базиса
относительно базиса  – векторное пространство векторов плоскости Р.
– векторное пространство векторов плоскости Р. – базис
– базис 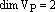 ,
, 
 , – разложение вектора
, – разложение вектора  по базису
по базису 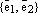 ,
,  – координаты вектора относительно базиса
– координаты вектора относительно базиса  – векторное пространство векторов в пространстве точек S.
– векторное пространство векторов в пространстве точек S.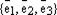 – базис
– базис  ,
, 
 – разложение вектора
– разложение вектора  по базису
по базису 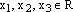 – координаты вектора
– координаты вектора  , то
, то 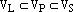 и можно выбрать базис
и можно выбрать базис  и
и  .
.
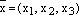 .
.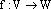 называют изоморфизмом векторного пространства
называют изоморфизмом векторного пространства  в векторное пространство
в векторное пространство 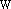 , если отображение f является биекцией (т.е. взаимно однозначным соответствием).Определение. Если существует изоморфизм
, если отображение f является биекцией (т.е. взаимно однозначным соответствием).Определение. Если существует изоморфизм 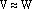 .
. является подпространством пространства V тогда и только тогда, когда W замкнуто относительно сложения векторов и умножения их на скаляры. Иными словами, выполняются следующие два условия:
является подпространством пространства V тогда и только тогда, когда W замкнуто относительно сложения векторов и умножения их на скаляры. Иными словами, выполняются следующие два условия:
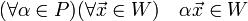
 подпространствU и W является векторным пространством.
подпространствU и W является векторным пространством.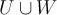 пространств Uи W не обязано быть векторным пространством.
пространств Uи W не обязано быть векторным пространством.
 вV — это наименьшее подпространство, содержащее все
вV — это наименьшее подпространство, содержащее все  , то есть
, то есть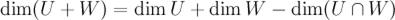
 с операциями сложения векторов и умножения их на скаляр, определенными следующей формулой:
с операциями сложения векторов и умножения их на скаляр, определенными следующей формулой:
 элементов векторного пространства
элементов векторного пространства 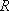 n над полем К называется множество всех линейных комбинаций этих элементов с коэффициентами из поля К. При этом сама совокупность
n над полем К называется множество всех линейных комбинаций этих элементов с коэффициентами из поля К. При этом сама совокупность 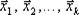 называется порождающей системой данной линейной оболочки, а сама линейная оболочка обозначается символом
называется порождающей системой данной линейной оболочки, а сама линейная оболочка обозначается символом 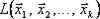
 , то любая линейно независимая система
, то любая линейно независимая система 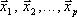 , является базисом линейной оболочки
, является базисом линейной оболочки