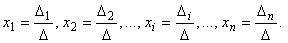Свойства ранга матрицы
1. Ранг матрицы, полученной транспонированием, равен рангу исходной матрицы. 2. Ранг матрицы останется неизменным, если вычеркнуть или приписать нулевую строку (т. е. строку, все элементы которой равны нулю) или нулевой столбец. Элементарные преобразования матрицы: 1) Отбрасывание нулевой строки (столбца). 2) Умножение всех элементов строки (столбца) на число 3) Изменение порядка строк (столбцов) матрицы. 4) Прибавление к каждому элементу одной строки (столбца) соответствующих элементов другой строки (столбца), умноженных на любое число. 5) Транспонирование матрицы. 10. Рассмотрим систему n линейных алгебраических уравнений относительно n неизвестных
Обозначим через А основную матрицу системы b. Определитель основной матрицы системы называется определителем системы. Определитель системы b имеет вид:
Если определитель матрицы системы отличен от нуля, Δ≠0, то решение системы определяется равенствами:
Теорема Крамера: Пусть Δ — определитель матрицы системы А, а Δj — определитель матрицы, получаемой из матрицы А заменой j-го столбца столбцом свободных членов. Тогда, если Δ ≠ 0., то система имеет единственное решение, определяемое по формулам:
где Δ — определитель матрицы системы и Δk — определитель матрицы, получаемой из матрицы системы заменой k–ого столбца столбцом свободных членов.(без доказательства)
|

 .
.