Умножение матрицы  на матрицу
на матрицу 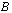 определено, когда число столбцов первой матрицы равно числу строк второй (условие согласованности). Тогда произведением матриц
определено, когда число столбцов первой матрицы равно числу строк второй (условие согласованности). Тогда произведением матриц 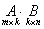 называется матрица
называется матрица 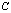 , каждый элемент которой
, каждый элемент которой  равен сумме произведений элементов
равен сумме произведений элементов  -ой строки матрицы
-ой строки матрицы  на соответствующие элементы
на соответствующие элементы 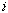 -го столбца матрицы
-го столбца матрицы 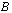 :
:
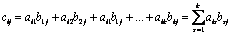 , где
, где 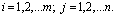
Пример. Вычислить произведение матриц  , где
, где 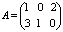 ,
,  .
.
Р е ш е н и е.
Найдем размер матрицы произведения  , следовательно, умножение возможно.
, следовательно, умножение возможно.
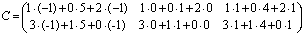 =
=  .
.
Свойства операций сложения и умножения матриц
1) 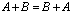 . 5)
. 5) 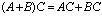 .
.
2) 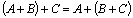 . 6)
. 6)  .
.
3) 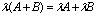 . 7)
. 7) 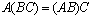 .
.
4)  .
.
8) 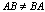 (в общем случае). Кроме того, если
(в общем случае). Кроме того, если  существует, то
существует, то 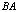 может вообще не существовать.
может вообще не существовать.
9) 
 , где
, где 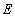 - единичная квадратная матрица.
- единичная квадратная матрица.
10) Произведение двух ненулевых матриц может равняться нулевой матрице, т.е. если 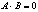 , то не следует, что
, то не следует, что 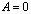 или
или  .
.
Пример.  ,
, 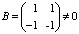 , но
, но  .
.

 на матрицу
на матрицу 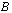 определено, когда число столбцов первой матрицы равно числу строк второй (условие согласованности). Тогда произведением матриц
определено, когда число столбцов первой матрицы равно числу строк второй (условие согласованности). Тогда произведением матриц 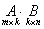 называется матрица
называется матрица 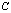 , каждый элемент которой
, каждый элемент которой  равен сумме произведений элементов
равен сумме произведений элементов  -ой строки матрицы
-ой строки матрицы 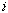 -го столбца матрицы
-го столбца матрицы 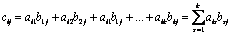 , где
, где 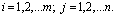
 , где
, где 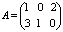 ,
,  .
. , следовательно, умножение возможно.
, следовательно, умножение возможно.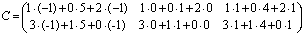 =
=  .
.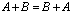 . 5)
. 5) 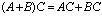 .
.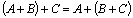 . 6)
. 6)  .
.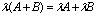 . 7)
. 7) 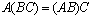 .
. .
.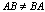 (в общем случае). Кроме того, если
(в общем случае). Кроме того, если  существует, то
существует, то 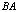 может вообще не существовать.
может вообще не существовать.
 , где
, где 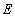 - единичная квадратная матрица.
- единичная квадратная матрица.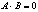 , то не следует, что
, то не следует, что 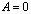 или
или  .
. ,
, 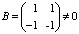 , но
, но  .
.


