Вычитание матриц.
Понятие матрицы. Виды матриц. Алгебраические операции над матрицами (умножение на число, сложение, умножение матриц) и их свойства. Транспонирование матрицы. Свойства транспонирования матрицы.
Матрицы широко применяются для описания экономических объектов и процессов. Элементами матрицы могут быть числа, буквы (символы) и другие объекты. Матрицы обозначают прописными (заглавными) буквами A, B, C, …, элементы матрицы – строчными буквами с двойной индексацией aij, где i - номер строки, j - номер столбца: Виды матриц: 1) Матрица-строка: 2) Матрица-столбец: 3) Нулевая матрица: 4) Квадратная матрица – если 5) Диагональная матрица (напр. 3-го порядка, где 6) Единичная матрица (например, 3-го порядка) Операции над матрицами 1. Умножение матрицы на число. Произведением матрицы A на число Пример. Вычислить Если 2. Сложение матриц. Суммой матриц Пример. Вычислить С = А + В, если Р е ш е н и е: Вычитание матриц. Разность матриц одинакового размера определяется как
|
Определение. Матрицей размера 
называется прямоугольная таблица, содержащая m строк и n столбцов.
;
;
;
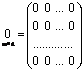(например n = 2 ):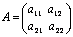 
;
любые числа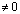 
): 
;
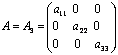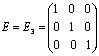
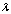называется матрица 
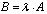,элементы которой 
для 
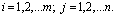
, если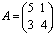 
. Р е ш е н и е: 
.
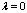, то 
(нулевая матрица того же размера).
и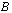 
одинакового размера 
называется матрица 
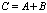, элементы которой 
для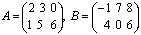 
.
.
.
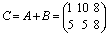