1)Даны: Ax+By+Cz+D=0 и 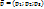 .
. 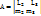 B=
B= 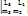 C=
C=  . Пусть Р
. Пусть Р  , тогда Р компланарен с
, тогда Р компланарен с  , и
, и  , то есть
, то есть 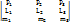 =0;
=0;  ;
; 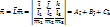 .
.  . Для того, чтобы была параллельность плоскости надо, чтобы
. Для того, чтобы была параллельность плоскости надо, чтобы 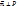 относительно декартовой системе координат (4);
относительно декартовой системе координат (4);  ;
; 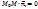 . Уравнение плоскости: Если вектор имеет координаты
. Уравнение плоскости: Если вектор имеет координаты 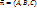 , то получим
, то получим 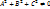
 этот вектор не параллелен плоскости. 2)Общее уравнение плоскости: Ax+By+Cz+D=0, где
этот вектор не параллелен плоскости. 2)Общее уравнение плоскости: Ax+By+Cz+D=0, где 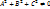 . Частные случаи общего уравнения плоскости: 1. Если D = 0, то плоскости удовлетворяет точка О(0;0;0). Плоскость проходит через начало координат. 2. Если С = 0, то имеем уравнение Ax+By+D=0. Нормальный вектор
. Частные случаи общего уравнения плоскости: 1. Если D = 0, то плоскости удовлетворяет точка О(0;0;0). Плоскость проходит через начало координат. 2. Если С = 0, то имеем уравнение Ax+By+D=0. Нормальный вектор 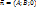 , перпендикулярен оси Οz. Плоскость параллельна оси Οz; если B = 0 — параллельна оси Оу, А = 0 — параллельна оси Ох. 3. Если С = D = 0, то плоскость проходит через О(0;0;0) параллельно оси Οz, т. е. плоскость Ax+By=0 проходит через ось Οz. Аналогично, уравнениям By+Cz=0 и Ax+ Cz=0 отвечают плоскости, проходящие соответственно через оси Ох и Оу. 4. Если А = В = 0, то плоскость параллельна плоскости Оху. Аналогично, уравнениям Ax=D=0 и By+D=0 отвечают плоскости, соответственно параллельные плоскостям Oyz и Οxz.. 5. Если A = B = D = 0, то уравнение примет вид Сz=0, т. е. z = 0. Это уравнение плоскости Оху. Аналогично: у = 0 — уравнение плоскости Οxz; x = О — уравнение плоскости Oyz.. 3) P(x y z)= Ax+By+Cz+D.
, перпендикулярен оси Οz. Плоскость параллельна оси Οz; если B = 0 — параллельна оси Оу, А = 0 — параллельна оси Ох. 3. Если С = D = 0, то плоскость проходит через О(0;0;0) параллельно оси Οz, т. е. плоскость Ax+By=0 проходит через ось Οz. Аналогично, уравнениям By+Cz=0 и Ax+ Cz=0 отвечают плоскости, проходящие соответственно через оси Ох и Оу. 4. Если А = В = 0, то плоскость параллельна плоскости Оху. Аналогично, уравнениям Ax=D=0 и By+D=0 отвечают плоскости, соответственно параллельные плоскостям Oyz и Οxz.. 5. Если A = B = D = 0, то уравнение примет вид Сz=0, т. е. z = 0. Это уравнение плоскости Оху. Аналогично: у = 0 — уравнение плоскости Οxz; x = О — уравнение плоскости Oyz.. 3) P(x y z)= Ax+By+Cz+D.
Плоскость П разделяет пространство на 2 полупространства. Пусть 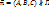

 ,
,  . Возьмем М, так, что
. Возьмем М, так, что  и продолжим его до пересечения с плоскостью
и продолжим его до пересечения с плоскостью  , тогда
, тогда 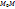 можно Записать как
можно Записать как  ,
,  .
.  - если одинаково направлены,
- если одинаково направлены, 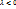 - если противоположно направлены
- если противоположно направлены
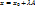


Подставим в P(x y z)= 

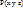 совпадает со знаком
совпадает со знаком  . Если
. Если  - одно полупространство,
- одно полупространство, 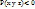 - второе полупространство.
- второе полупространство.