Взаимное расположение двух плоскостей.
1).
Необходимое и достаточное условие перпендикулярности двух плоскостей:
20. Различные способы задания прямой в пространстве. Прямая и плоскость. 2 прямые в пространстве. Угол между двумя прямыми. Замечание. Прямую в пространстве невозможно задать одним уравнением. Для этого требуется система двух или более уравнений. Первая возможность составить уравнения прямой в пространстве – представить эту прямую как пересечение двух непараллельных плоскостей, заданных уравнениями A1x+B1y+C1z+D1= 0 и A2x+B2y+C2z+D2 =0, где коэффициенты A1,B1,C1 и A2,B2,C2 не пропорциональны: A1x+B1y+C1z+D1 =0; A2x+B2y+C2z+D2 =0.Однако при решении многих задач удобнее пользоваться другими уравнениями прямой, содержащими в явной форме некоторые ее геометрические характеристики.Составим уравнения прямой, проходящей через точку М0(x0,y0,z0) параллельно вектору a ={l,m,n}.Определение. Любой ненулевой вектор, параллельный данной прямой, называется ее направляющим вектором. Для любой точки М(x,y,z), лежащей на данной прямой, вектор М0М = { x - x0,y - y0,z - z0) коллинеарен направляющему вектору а. Поэтому имеют место равенства: называемые каноническими уравнениями прямой в пространстве. В частности, если требуется получить уравнения прямой, проходящей через две точки: М1(х1, у1, z1) и M2(x2, y2, z2), направляющим вектором такой прямой можно считать вектор М1М 2 = { x2 – x1, y2 - y1, z2 - z1 }, и уравнения (8.11) принимают вид: Угол между прямыми. Угол между прямой и плоскостью. Угол между прямыми в пространстве равен углу между их направляющими векторами. Поэтому, если две прямые заданы каноническими уравнениями вида Условием параллельности прямой и плоскости является при этом условие перпендикулярности векторов n и а: Al + Bm + Cn = 0, а условием перпендикулярности прямой и плоскости – условие параллельности этих векторов: A/l = B/m = C/n.
21. каноническое уравнение эллипса. Свойства. называется линия, которая в некоторой декартовой прямоугольной системе координат определяется каноническим уравнением x2/a2 + y2/b2 = 1, при условии a≥b>0. Из уравнения следует, что для всех точек эллипса │x│≤ a и │у│≤ b. Значит, эллипс лежит в прямоугольнике со сторонами 2а и 2Ь. Точки пересечения эллипса с осями канонической системы координат, имеющие координаты (а, 0), (-а, 0), (0, b) и (0, -b), называются вершинами эллипса. Числа а и b называются соответственно большой и малой полуоси. С1. Оси канонической системы координат являются осями симметрии эллипса, а начало канонической системы - его центром симметрии.Внешний вид эллипса проще всего описать сравнением с окружностью радиуса а с центром в центре эллипса: х2 +у2 =а2. При каждом х таком, что I х I < а, найдутся две точки эллипса с ординатами ±b√1-x2/a2 и две точки окружности с ординатами ±a√1-x2/ а2 Пусть точке эллипса соответствует точка окружности с ординатой того же знака. Тогда отношение ординат соответствующих точек равно b/a. Итак, эллипс получается из окружности таким сжатием ее к оси абсцисс, при котором ординаты всех точек уменьшаются в одном и том же отношении b/a. С эллипсом связаны две замечательные точки, называемые его фокусами. Пусть по определению с2=a2 – b2 и c≥0.Фокусами называются точки F1 и F2 с координатами (с, 0) и (-с, 0) в канонической системе координат. Отношение e=c/a называется эксцентриситетом эллипса. Отметим, что
22. Каноническое уравнение гиперболы. Свойства. Гиперболой мы назвали линию, которая в некоторой декартовой прямоугольной системе координат определяется каноническим уравнением x2/a2 - y2/b2 = 1. Из этого уравнения видно, что для всех точек гиперболы │x│≥a, т.е. все точки гиперболы лежат вне вертикальной полосы ширины 2а. Ось абсцисс канонической системы координат пересекает гиперболу в точках с координатами (а, 0) и (-а, 0), называемых вершинами гиперболы. Ось ординат не пересекает гиперболу. Таким образом, гипербола состоит из двух не связанных между собой частей. Они называются ее ветвями. Числа а и Ь называются соответственно вещественной и мнимой полуосями гиперболы.C1. Для гиперболы оси канонической системы координат являются осями симметрии, а начало канонической системы - центром симметрии.Для исследования формы гиперболы найдем ее пересечение с произвольной прямой, проходящей через начало координат. Уравнение прямой возьмем в виде у = кх, поскольку мы уже знаем, что прямая х= 0 не пересекает гиперболу. Абсциссы точек перечения находятся из уравнения x2/a2 – k2x2/b2 = 1. Поэтому, если b2 – a2k2>0, то x = ± ab / √b2 – a2k2. Это позволяет указать координат точек пересечения (аb/u, аbк/u) и (-аb/и,-аbк/u),где обозначено u = (b2 - а2к2)1/2. Прямые с уравнениями у = Ьх/а и у = -bх/а в канонической системе координат называются асимптотами гиперболы. C2. Произведение расстояний от точки гиперболы до асимптот постоянно и равно а2b2 /(а2 + b2). C3. Если точка движется по гиперболе так, что ее абсцисса по абсолютной величине неограниченно возрастает, то расстояние от точки до одной из асимптот стремится к нулю. Введем число с, положив с2=а2+b2 и с > 0. Фокусами гиперболы называются точки F1 u F2 c координатами (c, 0) и (-с, 0) в канонической системе координат. Отношение е = с/а, как и для эллипса, называется эксцентриситетом. У гиперболы е > 1. C4. Расстояния от произвольной точки М (х, у) на гиперболе до каждого из фокусов следующим образом зависят от ее абсциссы х: r1=│F1M│=│a-ex│, r2 =│F2M│=│a+ex│. C5. Для того чтобы точка М лежала на гиперболе, необходимо и достаточно, чтобы разность ее расстояний до фокусов по абсолютной величине равнялась вещественной оси гиперболы 2а. Директрисами гиперболы называются прямые, задаваемые в канонической системе координат уравнениями x=a/
23. Каноническое уравнение параболы. Свойства. мы назвали линию, которая в некоторой декартовой прямоугольной системе координат определяется каноническим уравнением y2 =2рх, при условии р > 0. Из уравнения вытекает, что для всех точек параболы x≥0. Парабола проходит через начало канонической системы координат. Эта точка называется вершиной параболы. Фокусом параболы называется точка F с координатами (р/ 2, 0) в канонической системе координат. Директрисой параболы называется прямая с уравнением х=-р/2 в канонической системе координат. C1. Расстояние от точки М (х, у), лежащей на параболе, до фокуса равно r=x+p/2. C2. Для того чтобы точка М лежала на параболе, необходимо и достаточно, чтобы она была одинаково удалена от фокуса и от директрисы, этой параболы. Параболе приписывается эксцентриситет е = 1. В силу этого соглашения формула r/d=e верна и для эллипса, и для гиперболы, и для параболы. Выведем уравнение касательной к параболе в точке М0(х0,y0), лежащей на ней, имеет вид yy0 = p(x+x0). C3 Касательная к параболе в точке Мо есть биссектриса угла, смежного с углом между отрезком, который соединяет Мо с фокусом, и лучом, выходящим из этой точки в направлении оси параболы.
24. Алгебраические линии. Задать алгебраические линии на плоскость,значит некоторое алгебраическое ур-ие вида F(x,y)=0 и некоторая аффинная система координат окружности на плоскости, тогда те и только те M(x,y),координаты которых удовлетворяют уравнению,считают лежами на данном уравнении.Аналогично задаются уравнения для поверхности в пространстве.Задать алгебр.ур-ие вида F(x,y,z)=0(z) с 3 переменными и некоторую систему координат OXYZтолько те и те точки F(x,y,z)=0(z) являются уравнением плоскости. При этом мы считаем, что два ур-ия определяют одну и туже линию или поверхность т. и т. т.,когда одно из этих ур-ий получается из другого умножением на некоторый числовой множитель лямбда 25. Понятие алгебраической поверхности. Изучениепроизвольных множеств точек-задача совершенно необъятная.Опр.Алгебраической поверхностью называется множество точек,которое в какой-нибудь декартовой системе координат может быть задано уравнением вида
26. Цилиндрические поверхности 2-го порядка. Пусть плоскость П дана некоторая прямая 2-го порядка и связка параллельных прямых d таких, что для любого d не параллельного П, тогда множество φ всех точек пространства принадлежащих тем прямым связки, которые пересекают линию γ называется направляющими, а прямые пересекающие φ – образующие. Выведем уравнение цилиндрической поверхности, относительно аффинной системы координат. Пусть в некоторой плоскости П лежит некоторая К, уравнение которой F(x,y)=0, в имеет направление а(а1а2а3) d параллелен а. Точка М(x,y,z) лежит на какой-то образующей, а N(x’y’o) – точка пересечения этой образующей с плоскостью П. Вектор MN будет коллинеарен с ta следовательно MN=ta, x’=x+a1t; y’=y+a2t; 0=z+a3t следовательно t= -z/a3, тогда x’=x- (a1z)/a3; y’=y- (a2z)/a3 F(x’y’)=0 F(x- (a1z)/a3; y- (a2z)/a3. Теперь ясно, что уравнение F(x,y)=0 есть уравнение цилиндра с образующими параллельными оси Оy, а F(y,z)=0 с образующими параллельными оси Ох. Частный случай: Пусть прямая связки а параллельна (о,z) следовательно а1=0 а2=0 а3≠0 F(x,y)=0, поэтому сколько линий второго порядка, столько и цилиндров. Поверхности: 1. Эллиптический цилиндр x2/a2+y2/b2=1 2. Гиперболический цилиндр x2/a2-y2/b2=1 3. Параболический цилиндр y2=2πx 4. Пара пересекающихся плоскостей x2/a2-y2/b2=0 5. Пара параллельных плоскостей x2/a2=1
27. Канонические поверхности 2-го порядка. Поверхность, на которой имеется точка Мо, обладающая тем свойством, что вместе с каждой точкой Мо≠M содержит прямую (МоМ), такая поверхность называется канонической или конусом. Мо – вершина конуса, а прямые – ее образующие. Функция F(x,y,z)=0 называется однородной, если F(tx,ty,tz)=φ(t) F(x,y,z), где φ(t) – функция от t. Теорема. Если F(x,y,z) однородная функция, то поверхность, определяемая этим уравнением есть каноническая поверхность с вершиной в начале координат. Док-во. Пусть задана аффинная система координат и от нее задано каноническое уравнение с центром F(x,y,z)=0. Рассмотрим уравнение с вершиной в точке O M(x,y,z)=0, тогда всякая точка OM из F будет иметь вид M1(tx,ty,tz) на канонической поверхности. MoM(x,y,z), раз удовлетворяет поверхности, то F(tx,ty,tz)=0 функция однородная φ(t) F(x,y,z)=0 следовательно поверхность каноническая. Кривые 2-го порядка явл сечениями в конечной поверхности плоскостей x2+y2-z2=0/ При сечении канонических поверхностей плоскостями получаем в сечении следующие линии: а) плоскость проходящую через точку или пара слившихся прямых и пара пересекающихся прямых. Б) плоскость не проходит через вершину конуса следовательно получаем в сечении либо эллипс, либо гиперболу, либо параболу. 28. Поверхности вращения. Пусть в 3-мерном пространстве дан декартовый репер. Плоскость П проходит через Oz, в плоскости Ozy задана γ и угол xOy=φ γ имеет вид u=f(z). Возьмем точку M из γ относительно репера Oxyz. γ – описанная окружность γМ по всем точкам М из γ называется отображением. Сечением поверхности вращения плоскости, проходящей через ось вращения называется меридианом. Сечением поверхности вращения плоскости перпендикулярной оси вращения называется параллельной. Уравнение поверхности вращения
29. Эллипсоиды. Поверхность, которая получается при вращении эллипса вокруг его осей симметрии. Направив вектор е3 сначала вдоль малой оси эллипса, а затем вдоль большой оси, мы получим ур-я эллипса в следующих видах: Каждую точку М (x, y, z) на сжатом эллипсоиде вращения сдвинем к плоскости y=0 так, чтобы расстояние от точки до этой плоскости уменьшалось в постоянном для всех точек отношении λ<1. После сдвига точка попадет в положение M’ (x’, y’, z’), где x’=x, y’=λy, z’=z. Таким образом, точки эллипсоида вращения переходят в точки поверхности с ур-ем 30. Гиперболоиды. Однополостный гиперболоид вращения – это поверхность вращения гиперболы вокруг той оси, которая ее не пересекает. По формуле Двуполостный гиперболоид. Двуполостный гиперболоид вращения – это поверхность, получаемая вращением гиперболы 31. Параболоиды. Эллиптический параболоид. Вращая параболу x2=2pz вокруг ее оси симметрии, мы получаем поверхность с ур-ем x2+y2=2pz. Она называется параболоидом вращения. Сжатие к плоскости y=0 переводит параболоид вращения в поверхность, ур-е которой приводится к виду
32. Комплексные числа. Алгебраическая форма комплексного числа. Комплексным числом называется выражение вида z = х + iу, где х и у — действительные числа, i — мнимая единица. Число х называется действительной частью числа z и обозначается Rе(z), а число у — мнимой частью числа z и обозначается Im(z). Числа z = х + iу и z = х - iу называются сопряженными. Два комплексных числа z1 = х1 + iу1 и z2 = х2 + iу2 называются равными, если равны их действительные и мнимые части. В частности i2=-1. Арифметические операции на множестве комплексных чисел определяются следующим образом. 1. Сложение: z1+z2=x1+x2+i(y1+y2); 2.Вычитание: z1-z2=x1-x2+i(y1-y2); 3.Умножение: z1z2=(x1x2-y1y2)+i(x1y2+x2y1); Деление: z1/z2=((x1x2+y1y2)+i(x2y1- x1y2))/x22+y22. Для представления к.ч. служат точки координатной плоскости Оху. Плоскость называется комплексной, если каждому к.ч. z = х + iу ставится в соответствие точка плоскости z(х, у), причем это соответствие взаимно однозначное. Оси Ох и Оу, на которых расположены действительные числа z=x+0i=x и чисто мнимые числа z=0+iy=iy, называются соответсвенно действительной и мнимой осями 33. Тригонометрическая форма комплексного числа. Формула Муавра. Если вещественную x и мнимую y части комплексного числа выразить через модуль r = | z | и аргумент j(x=r cosj,y=r sinj), то всякое комплексное число z, кроме нуля, можно записать в тригонометрической форме z=r(cosj+isinj). Особенности тригонометрической формы: 1)первый множитель неотрицательное число, r³0; 2)записаны косинус и синус одного и того же аргумента; 3) мнимая единица умножена на sinj. Также может быть полезна показательная форма записи комплексных чисел, тесно связанная с тригонометрической через формулу Эйлера: z=reij. Где eij — расширение экспоненты для случая комплексного показателя степени. Формула, позволяющая возводить в степень комплексное число, представленное в тригонометрической форме. Формула Муавра имеет вид: z=[r(cosj+isinj)]n=rn(cosnj+isin nj), где r — модуль, а j — аргумент комплексного числа.
34. Операции над многочленами. Алгоритм Евклида. Общий вид уравнения n-ой степени: a0xn+a1xn-1+…+an-1x+an=0 (1). Определяется набор коэффициентов. (а0,а1,…,an-1,an)-произвольные комплексные числа. Рассмотрим левую часть (1): a0xn+a1xn-1+…+an-1x+an-многочлены n-ой степени. Два многочлена f(x) и g(x) будим считать равными или тождественно равными, если равны коэффициенты при одинаковых степенях. Любой многочлен определяется набором коэффициентов. Определим операции сложения и умножения над многочленами: f(x)=a0+a1x+…+anxn; g(x)=b0+b1x+…+bsxs n³s; f(x)+g(x)=c0+c1x+…+cnxn-1+cn; ci=ai+bi если i=0,1…n; i>s bi=0; f(x)*g(x)=d0+d1x+…+dn+sxn+s;
1) 2)
35.Делитель многочленов. НОД. Пусть даны два ненулевых многочлена f(x) и j(x)с комплексными коэффициентами. Если остаток rk-2(x)=rk-1(x)qk(x)+rk(x) rk-1(x)=r2(x)+qk(x) rk(x)-НОД. Докажем. rk(x) делитель rk-1(x)®он делитель rk-2(x)…®он делитель g(x)®делитель f(x). g(x)g1(x) делится на rk(x)® f(x)- g(x) g1(x) делится на rk(x)® r1(x) делится на rk(x)® r2(x) делится на rk(x)®… qk(x): rk(x) делится на rk(x).
|

 2)
2) 
 не меньше 1, так хотя бы 1 элемент отличен от нуля. Пусть 1 и 2 пересекаются
не меньше 1, так хотя бы 1 элемент отличен от нуля. Пусть 1 и 2 пересекаются  они имеют общую линию
они имеют общую линию  они имеют общую систему
они имеют общую систему  . Пусть 1 и 2 параллельны:
. Пусть 1 и 2 параллельны:  ,
,  . Если декартовая система координат, то
. Если декартовая система координат, то 
 - нормальные вектора. Косинус угла между двумя векторами:
- нормальные вектора. Косинус угла между двумя векторами:
 или
или 

 - уравнения прямой, проходящей через две данные точки. Если же принять каждую из равных дробей в уравнениях за некоторый параметр t, можно получить так называемые параметрические уравнения прямой:
- уравнения прямой, проходящей через две данные точки. Если же принять каждую из равных дробей в уравнениях за некоторый параметр t, можно получить так называемые параметрические уравнения прямой: . Для того, чтобы перейти от уравнений к каноническим или параметрическим уравнениям прямой, требуется найти направляющий вектор этой прямой и координаты любой точки, принадлежащей ей. Направляющий вектор прямой ортогонален нормалям к обеим плоскостям, следовательно, он коллинеарен их векторному произведению. Поэтому в качестве направляющего вектора можно выбрать [ n1n2 ] или любой вектор с пропорциональными координатами. Чтобы найти точку, лежащую на данной прямой, можно задать одну ее координату произвольно, а две остальные найти из уравнений, выбрав их так, чтобы определитель из их коэффициентов не равнялся нулю.
. Для того, чтобы перейти от уравнений к каноническим или параметрическим уравнениям прямой, требуется найти направляющий вектор этой прямой и координаты любой точки, принадлежащей ей. Направляющий вектор прямой ортогонален нормалям к обеим плоскостям, следовательно, он коллинеарен их векторному произведению. Поэтому в качестве направляющего вектора можно выбрать [ n1n2 ] или любой вектор с пропорциональными координатами. Чтобы найти точку, лежащую на данной прямой, можно задать одну ее координату произвольно, а две остальные найти из уравнений, выбрав их так, чтобы определитель из их коэффициентов не равнялся нулю.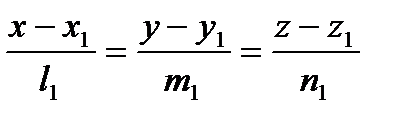 и
и 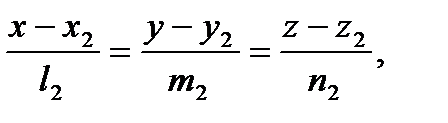 косинус угла между ними можно найти по формуле:
косинус угла между ними можно найти по формуле: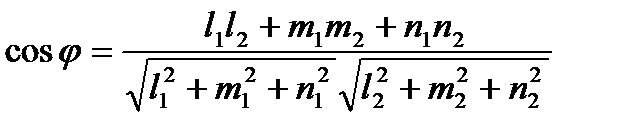 . Условия параллельности и перпендикулярности прямых тоже сводятся к соответствующим условиям для их направляющих векторов:
. Условия параллельности и перпендикулярности прямых тоже сводятся к соответствующим условиям для их направляющих векторов: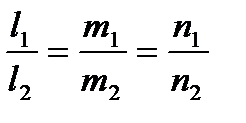 - условие параллельности прямых,
- условие параллельности прямых, - условие перпендикулярности прямых. Угол φ между прямой, заданной каноническими уравнениями
- условие перпендикулярности прямых. Угол φ между прямой, заданной каноническими уравнениями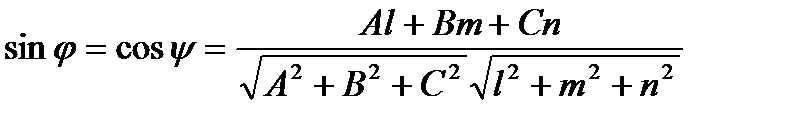
 < 1. С2. Расстояние от произвольной точки М (х, у), лежащей на эллипсе, до каждого из фокусов является линейной функцией от ее абсциссы х: R1=│F1M│=a-
< 1. С2. Расстояние от произвольной точки М (х, у), лежащей на эллипсе, до каждого из фокусов является линейной функцией от ее абсциссы х: R1=│F1M│=a-  , x=-a/
, x=-a/ 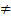 0.
0. +…+
+…+  =0,где все показатели степени-целые неотрицательные числа.Наибольшая из сумм(разумеется,здесь имеется в виду наибольшая из сумм,фактически входящих в уравнение,т.е.предполагается,что после приведения подобных членов найдется хотя бы одно слагаемое с ненулевым коэффициентом,имеющее такую сумму показателей.)
=0,где все показатели степени-целые неотрицательные числа.Наибольшая из сумм(разумеется,здесь имеется в виду наибольшая из сумм,фактически входящих в уравнение,т.е.предполагается,что после приведения подобных членов найдется хотя бы одно слагаемое с ненулевым коэффициентом,имеющее такую сумму показателей.)  +
+  +
+  ,….,
,….,  +
+  +
+  называется степенью уравнения,а также порядком алгебраической поверхности.Это определение означает,в частности,что сфера,уравнение которой в декартовой прямоугольной системе координат имеет вид (
называется степенью уравнения,а также порядком алгебраической поверхности.Это определение означает,в частности,что сфера,уравнение которой в декартовой прямоугольной системе координат имеет вид (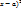 +(
+( +(
+( =
=  ,является алгебраической поверхностью второго порядка.Теорема.Алгебраическая поверхность порядка p в любой декартовой системе координат может быть задана уравнением вида
,является алгебраической поверхностью второго порядка.Теорема.Алгебраическая поверхность порядка p в любой декартовой системе координат может быть задана уравнением вида  x2+y2=f2(z) – уравнение поверхности вращения. 1) Если угол φ=0, то γ лежит в плоскости xOz, x2+y2=f2(z) 2) γ лежит в плоскости xOy и уравнение ее y=g(x), тогда y2+z2=g2(x) 3) γ лежит в плоскости yOz и уравнение ее z=h(y), тогда z2+x2=h2(y)
x2+y2=f2(z) – уравнение поверхности вращения. 1) Если угол φ=0, то γ лежит в плоскости xOz, x2+y2=f2(z) 2) γ лежит в плоскости xOy и уравнение ее y=g(x), тогда y2+z2=g2(x) 3) γ лежит в плоскости yOz и уравнение ее z=h(y), тогда z2+x2=h2(y) . В силу формулы
. В силу формулы  ур-я соответствующих поверхностей вращения будут
ур-я соответствующих поверхностей вращения будут  = 1 (a>c). Поверхности с такими ур-ями называются сжатым (а) и втянутым (б) эллипсоидами вращения.
= 1 (a>c). Поверхности с такими ур-ями называются сжатым (а) и втянутым (б) эллипсоидами вращения. , где b=λa. Поверхность, которая в некоторой декартовой системе координат имеет это ур-е, называется эллипсоидом (в). Если случайно окажется, что b=c, мы получим снова эллипсоид вращения, но уже вытянутый. Эллипсоид, так же, как и эллипсоид вращения, из которого он получен, представляет собой замкнутую ограниченную поверхность. Из уравнения видно, чо начало канонической системы координат – центр симметрии эллипсоида, а координатные плоскости – его плоскости симметрии. Эллипсоид можно получить из сферы x2+y2+z2=a2 сжатиями к плоскостям у=0 и z =0 в отношениях λ=b/a и μ=с/а.
, где b=λa. Поверхность, которая в некоторой декартовой системе координат имеет это ур-е, называется эллипсоидом (в). Если случайно окажется, что b=c, мы получим снова эллипсоид вращения, но уже вытянутый. Эллипсоид, так же, как и эллипсоид вращения, из которого он получен, представляет собой замкнутую ограниченную поверхность. Из уравнения видно, чо начало канонической системы координат – центр симметрии эллипсоида, а координатные плоскости – его плоскости симметрии. Эллипсоид можно получить из сферы x2+y2+z2=a2 сжатиями к плоскостям у=0 и z =0 в отношениях λ=b/a и μ=с/а.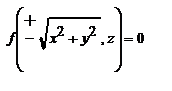 мы получаем уравнение этой поверхности (рис. 48). В результате сжатия однополостного гиперболоида вращения к плоскости y=0 мы получаем однополостный гиперболоид с ур-ем
мы получаем уравнение этой поверхности (рис. 48). В результате сжатия однополостного гиперболоида вращения к плоскости y=0 мы получаем однополостный гиперболоид с ур-ем 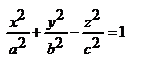 . Интересное св-во однополостного гиперболоида – наличие у него прямолинейных образующих. Так называются прямые линии, всеми точками лежащие на поверхности. Через каждую точку однопол гиперболоида проходят две прямолинейные образующие, ур-я которых можно получить следующим образом. Ур-е (8) можно переписать в виде
. Интересное св-во однополостного гиперболоида – наличие у него прямолинейных образующих. Так называются прямые линии, всеми точками лежащие на поверхности. Через каждую точку однопол гиперболоида проходят две прямолинейные образующие, ур-я которых можно получить следующим образом. Ур-е (8) можно переписать в виде 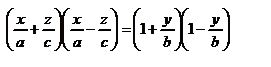 . Рассмотрим прямую линию с ур-ями μ
. Рассмотрим прямую линию с ур-ями μ 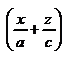 =λ
=λ  , λ
, λ 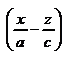 =μ
=μ  (9), где λ и μ – некоторые числа (λ2+μ2≠0). Координаты каждой точки прямой удовлетворяют обоим ур-ям, а следовательно и ур-ю (8), которое получается почленным перемножением. Поэтому каковы бы ни были λ и μ прямая с ур-ями (9) лежит на однополостном гиперболоиде. Таким образом, система (9) определяет семейство прямолинейных образующих. Если вместе с гиперболой мы будем вращать ее асимптоты, то они опишут прямой круговой конус, называемый асимптотическим конусом гиперболоида вращения. Пр и сжатии гиперболоида вращения его асимптотический конус сжимается в асимптотический конус общего однополостного гиперболоида.
(9), где λ и μ – некоторые числа (λ2+μ2≠0). Координаты каждой точки прямой удовлетворяют обоим ур-ям, а следовательно и ур-ю (8), которое получается почленным перемножением. Поэтому каковы бы ни были λ и μ прямая с ур-ями (9) лежит на однополостном гиперболоиде. Таким образом, система (9) определяет семейство прямолинейных образующих. Если вместе с гиперболой мы будем вращать ее асимптоты, то они опишут прямой круговой конус, называемый асимптотическим конусом гиперболоида вращения. Пр и сжатии гиперболоида вращения его асимптотический конус сжимается в асимптотический конус общего однополостного гиперболоида.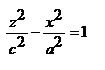 вокруг той оси, которая ее пересекает. По формуле
вокруг той оси, которая ее пересекает. По формуле  мы получаем ур-е двуполостного гиперболоида вращения
мы получаем ур-е двуполостного гиперболоида вращения  В результате сжатия этой поверхности к плоскости y=0 получается поверхность с ур-ем
В результате сжатия этой поверхности к плоскости y=0 получается поверхность с ур-ем 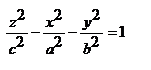 (12). Поверхность, которая в некоторой декартовой прямоугольной системе координат имеет ур-е вида (12), называет двуполостным гиперболоидом (рис. 49). Двум ветвям гиперболы здесь соответствуют две несвязанные между собой части («полости») поверхности. Асимптотический конус двуполостного гиперболоида определяется так же, как и для однополостного.
(12). Поверхность, которая в некоторой декартовой прямоугольной системе координат имеет ур-е вида (12), называет двуполостным гиперболоидом (рис. 49). Двум ветвям гиперболы здесь соответствуют две несвязанные между собой части («полости») поверхности. Асимптотический конус двуполостного гиперболоида определяется так же, как и для однополостного.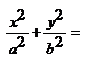 2z (14). Поверхность, которая имеет такое ур-е в некоторой декартовой прямоугольной системе координат, называется эллиптическим параболоидом. Гиперболический параболоид. По аналогии с ур-ем (14) мы можем написать ур-е
2z (14). Поверхность, которая имеет такое ур-е в некоторой декартовой прямоугольной системе координат, называется эллиптическим параболоидом. Гиперболический параболоид. По аналогии с ур-ем (14) мы можем написать ур-е 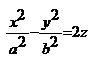 Поверхность, которая имеет такое ур-е в некоторой декартовой прямоугольной системе координат, называется гиперболическим параболоидом. Из канонического уравнения z= x2/a2 - y2/b2 гиперболического параболоида вытекает, что плоскости Охz и Оуz являются плоскостями симметрии. Ось Оz называется осью гиперболического параболоида.. Линии z=h пересечения гиперболического параболоида с плоскостями z=h представляют собой при h > 0 гиперболы x2/a*2 - y2/b*2 =1 с полуосями a*= a√h, b*=b√h, а при h<0 – сопряженные гиперболы для гипербол x2/a*2 - y2/b*2 =1 с полуосями a*= a√-h, b*=b√-h. Используя эти формулы, легко построить «карту» гиперболического параболоида. Как и в случае эллиптического параболоида, можно убедиться в том, что гиперболический параболоид может быть получен путем параллельного перемещения параболы, представляющей собой сечение плоскостью Охz (Оуz), когда ее вершина движется вдоль параболы, являющейся сечением параболоида плоскостью Оуz (Охz).
Поверхность, которая имеет такое ур-е в некоторой декартовой прямоугольной системе координат, называется гиперболическим параболоидом. Из канонического уравнения z= x2/a2 - y2/b2 гиперболического параболоида вытекает, что плоскости Охz и Оуz являются плоскостями симметрии. Ось Оz называется осью гиперболического параболоида.. Линии z=h пересечения гиперболического параболоида с плоскостями z=h представляют собой при h > 0 гиперболы x2/a*2 - y2/b*2 =1 с полуосями a*= a√h, b*=b√h, а при h<0 – сопряженные гиперболы для гипербол x2/a*2 - y2/b*2 =1 с полуосями a*= a√-h, b*=b√-h. Используя эти формулы, легко построить «карту» гиперболического параболоида. Как и в случае эллиптического параболоида, можно убедиться в том, что гиперболический параболоид может быть получен путем параллельного перемещения параболы, представляющей собой сечение плоскостью Охz (Оуz), когда ее вершина движется вдоль параболы, являющейся сечением параболоида плоскостью Оуz (Охz). ; d0=a0b0; d1=a0b1+a0b1; d2=a0b2+a1b1+a2b0. Степень произведения многочленов равна сумме и операции обладают свойствами: 1)ak+bk=bk+ak; 2)(ak+bk)+ck=ak+(bk+ck); 3)
; d0=a0b0; d1=a0b1+a0b1; d2=a0b2+a1b1+a2b0. Степень произведения многочленов равна сумме и операции обладают свойствами: 1)ak+bk=bk+ak; 2)(ak+bk)+ck=ak+(bk+ck); 3) 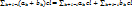 . Многочлен f(x) называется обратным
. Многочлен f(x) называется обратным  (x), если f(x)*
(x), если f(x)*  (x)=1. Во множестве многочленов операция деления не возможна. В Евклидовом пространстве для многочлена существует алгоритм деления с остатком. f(x) и g(x) существуют r(x) и q(x) определены однозначно.
(x)=1. Во множестве многочленов операция деления не возможна. В Евклидовом пространстве для многочлена существует алгоритм деления с остатком. f(x) и g(x) существуют r(x) и q(x) определены однозначно. 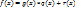 ;
;  ; f(x)=g(x);
; f(x)=g(x);  ;
;  . Степень правой части £ степени g(x), а степень левой части
. Степень правой части £ степени g(x), а степень левой части  отсюда
отсюда  отсюда – мы пришли к противоречию. Доказываем первую часть теоремы:
отсюда – мы пришли к противоречию. Доказываем первую часть теоремы: 
 . Домножим g(x) на такой многочлен, чтобы старшие коэффициенты умножались.
. Домножим g(x) на такой многочлен, чтобы старшие коэффициенты умножались.
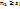





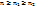 после k шагов.
после k шагов.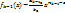

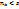
 ;
;  ;
; 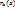 имеет меньшую степень q(x). Многочлен q(x)- частное от f(x), a r(x) –остаток от деления. Если f(x) и g(x) имеют действительные коэффициенты, то q(x) и r(x) – тоже действительные.
имеет меньшую степень q(x). Многочлен q(x)- частное от f(x), a r(x) –остаток от деления. Если f(x) и g(x) имеют действительные коэффициенты, то q(x) и r(x) – тоже действительные.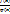 равен нулю, то говорят, что f(x) делится на j(x), если j(x) является делителем f(x). Cв-ва многочлена j(x): 1)Многочлен j(x) будет делителем f(x), если существует Y(х) и f(x)= j(x)* Y(х) (1). j(x)-делитель, Y(х) -частное. Пусть Y(х) удовлетворяет (1), тогда из предыдущей теоремы Y(х) является частным, а остаток равен 0. Если(1) выполняется, то j(x)-делитель, отсюда j(x)<= степени f(x). Основные св-ва делимости многочлена: 1)
равен нулю, то говорят, что f(x) делится на j(x), если j(x) является делителем f(x). Cв-ва многочлена j(x): 1)Многочлен j(x) будет делителем f(x), если существует Y(х) и f(x)= j(x)* Y(х) (1). j(x)-делитель, Y(х) -частное. Пусть Y(х) удовлетворяет (1), тогда из предыдущей теоремы Y(х) является частным, а остаток равен 0. Если(1) выполняется, то j(x)-делитель, отсюда j(x)<= степени f(x). Основные св-ва делимости многочлена: 1) 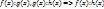 ; 2
; 2  f(x) и g(x) делятся на j(х), то
f(x) и g(x) делятся на j(х), то  делятся на j(x); 3)если
делятся на j(x); 3)если 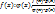 ; 4)если f1(x)..fk(x):j(x)®f1g1 +…+fkgk:j(x); 5) всякий многочлен делится на любой многочлен нулевой степени f(x)=a0xn+a1xn-1+an c
; 4)если f1(x)..fk(x):j(x)®f1g1 +…+fkgk:j(x); 5) всякий многочлен делится на любой многочлен нулевой степени f(x)=a0xn+a1xn-1+an c  ; 6) если f(x):j(x), то f(x):cj(x); 7)Многочлен cf(x) и только они будут делителями многочлена j(х), имеющие такую же степень, что и f(x); 8)f(x):g(x) и g(x):f(x), то g(x)=cf(x); 9)Всякий делитель одного из f(x) и cf(x), с¹0 будет делителем для другого. Опр-ние:Наибольший общий делитель (НОД). Многочлен j(х) будем называть НОД f(x) и g(x), если он делит каждого из них. Многочлены нулевой степени всегда являются НОД и являются взаимопростыми. НОД отличных от нуля многочленов f(x) и g(x) называется d(x), который явл. общим делителем и делится на любой другой делитель и общий этих многочленов. НОД f(x) и g(x)= (f(x):g(x)). Алгоритм нахождения НОД: Пусть степень g(x)<= степениf(x) f(x)=g(x)g1(x)+r1(x) g(x)=r1(x)q2(x)+r2(x)
; 6) если f(x):j(x), то f(x):cj(x); 7)Многочлен cf(x) и только они будут делителями многочлена j(х), имеющие такую же степень, что и f(x); 8)f(x):g(x) и g(x):f(x), то g(x)=cf(x); 9)Всякий делитель одного из f(x) и cf(x), с¹0 будет делителем для другого. Опр-ние:Наибольший общий делитель (НОД). Многочлен j(х) будем называть НОД f(x) и g(x), если он делит каждого из них. Многочлены нулевой степени всегда являются НОД и являются взаимопростыми. НОД отличных от нуля многочленов f(x) и g(x) называется d(x), который явл. общим делителем и делится на любой другой делитель и общий этих многочленов. НОД f(x) и g(x)= (f(x):g(x)). Алгоритм нахождения НОД: Пусть степень g(x)<= степениf(x) f(x)=g(x)g1(x)+r1(x) g(x)=r1(x)q2(x)+r2(x)


