Определители n-ого порядка. Теорема о знаке члена определителя.
Понятие определителя. Рассмотрим произвольную квадратную матрицу любого порядка п: С каждой такой матрицей свяжем вполне определенную численную характеристику, называемую определителем, соответствующим этой матрице. Если порядок п матрицы равен единице, то эта матрица состоит из одного элемента а11 и определителем первого порядка, соответствующим такой матрице, мы назовем величину этого элемента. Если далее порядок п матрицы равен двум, т. е. если эта матрица имеет вид Договоримся называть минором любого элемента aij матрицы n-го порядка определитель порядка п-1, соответствующий той матрице, которая получается из матрицы А в результате вычеркивания i-й строки и j-го столбца. Определителем порядка п, соответствующим матрице А, назовем число, равное Итак, по определению, Теорема о знаке члена определителя. Знак члена определителя ai1j1, ai1j1,… ainjn совпадает со знаком (-1)s+t, где S-число инверсий в перестановке i1,i2,…in t-число инверсий в перестановке j1,j2,…jn индексов столбцов.
40.Свойства определителей. 1°) Свойство равноправности строк и столбцов. Транспонированием любой матрицы или определителя называется операция, в результате которой меняются местами строки и столбцы с сохранением порядка их следования. В результате транспонирования матрицы А получается матрица, называемая транспонированной по отношению к матрице А и обозначаемая символом А'.при транспонировании величина определителя сохраняется, т. е. \А'\ = \А\. Это свойство непосредственно вытекает из теоремы о разложении определителя по j-тому столбцу (достаточно лишь заметить, что разложение определителя \А\ по первому столбцу тождественно совпадает с разложением определителя \А'\ по первой строке).2°) Свойство антисимметрии при перестановке двух строк (или двух с т о л б ц о в). Если две строки (два столбца) определителя поменять местами, то он сохранит свою абсолютную величину, но сменит свой знак на противоположный.
Считая, что п > 2, рассмотрим теперь определитель n-го порядка и предположим, что в этом определителе меняются местами две строки с номерами i1 u i2 Записывая формулу Лапласа разложения по этим двум строкам, будем иметь При перестановке местами строк с номерами i1 u i2 каждый определитель второго порядка 3°) Линейное свойство определителя. Будем говорить, что некоторая строка (а1, а2,…аn) является линейной комбинацией строк (b1, b2,…bn), (c1, c2,…cn),… (d1, d2,…dn) с коэффициентами В самом деле, при перестановке двух одинаковых строк, с одной стороны, определитель А не изменится, а с другой стороны, в силу свойства 2°) изменит знак на противоположный. Следствие 2. Умножение всех элементов некоторой строки (или некоторого столбца) определителя на число Следствие 5. Если к элементам некоторой строки (или некоторого столбца) определителя прибавить соответствующие элементы другой строки (другого столбца), умноженные на произвольный множитель А, то величина определителя не изменится. 4°) Свойство алгебраических дополнений соседних строк (или столбцов). Сумма произведений элементов какой-либо строки (или какого-либо столбца) определителя на соответствующие алгебраические дополнения элементов любой другой строки (любого другого столбца) равна нулю. Доказательство проведем для строк (для столбцов оно проводится аналогично). поскольку алгебраические дополнения
41. Теорема Лапласа. Дан определитель n-ого порядка, в нем зафиксировано k-строк 1 42. Правило Крамера. Число уравнений равно числу независимых.
Док-во: возьмём расширенную матрицу А* припишем сверху произвольную её строку
det
Тогда получим (если разложим верхнюю строку). А* Доказательство единственности: Пусть существуют 2 решения (
Имеет вид
43. Базисный минор. В матрице А размером (m*n) минор порядка r называется базисным, если он отличен т нуля и все минор r+1 порядка =0 или он не существует. r=min(m,n). Очевидно, что базисные миноры имеют один и тот же порядок. Столбцы и строки, на пересечении которых расположен базисный минор, называется базисными столбцами и строками. Рангом матрицы А называется порядок базисного минора, или самый большой порядок, для которого существуют отличные от нуля миноры. Ранг матрицы А обозначается так: RgA=r. Для нахождения ранга матрицы применяются элементарные преобразования: 1.Умножение строки на число
Приведение матрицы А к упрощенному виду. Матрица А (m*n) несколько первых столбцов могут оказаться ненулевыми, состоящими из одних нулей. Существует
________ _ - упрощенный вид
44. Теорема Кронекера-Капелли. Теорема:Для того чтобы линейна система a11x1+a12x2+…+a1nxn=b1, a21x1+a22x2+…+a2nxn=b2, ………………………………… am1x1+am2x2+…+amnxn=bm. (1) являлась совместной, необходимо и достаточно, чтобы ранг расширенной матрицы этой системы был равен рангу ее основной матрицы.
До-во: 1)Необходимость. Пусть система (1) совместна, т.е. существуют такие числа с1,с2,…сn, что справедливы равенства: a11c1+a12c2+…+a1ncn=b1, a21c1+a22c2+…+a2ncn=b2, ………………………............. am1c1+am2c2+…+amncn=bm. (3) Т.е. столбец свободных членов является линейной комбинацией столбцов матрицы системы и, следовательно, столбцов любого ее базисного минора. Поэтому добовление элементов этого столбца и любой строки расширенной матрицы к базисному минору даст нулевой определитель, т.е. RgA1=RgA. 2) Достаточность. Если RgA1=RgA, то любой базисный минор матрицы А является и базисным минором расширенной матрицы. Поэтому столбец свободных членов представляет собой линейную комбинацию столбцов этого базисного минора, и, следовательно, линейную комбинацию всех столбцов матрицы А. Если обозначить коэффициенты этой линейной комбинации с1,с2,…сn, то эти числа будут решением системы (1), т.е. эта система совместна. Теорема доказана.
45.Нахождение решений системы уравнений. Пусть дана совместная система: r- ранг системы: RgA=r, RgA*= r. Можем выбрать базисный минор расширенной матрицы так, чтобы он был расположен в основной матрице системы. Применяя элементарные преобразования, расширенню матрицу приведем к упрощенному виду. Тогда она перейдет к эквивалентному виду из r линейно-независимых уравнений. Предполагая, что базисный минор расположен в первых r столбцах.
………………………………………………………. (6)
В правой части-неизвестные, соответствующие столбцам выбранного базисного минора(неизвестые называются базисными), все остальные:
…………………………………… (7)
Предложение 1. Если
|

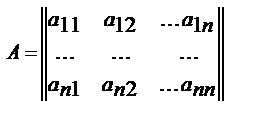
 , то определителем второго порядка, соответствующим такой матрице, назовем число, равное а11а22-а12а21 и обозначаемое одним из символов
, то определителем второго порядка, соответствующим такой матрице, назовем число, равное а11а22-а12а21 и обозначаемое одним из символов 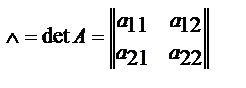 Итак, по определению
Итак, по определению 
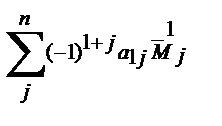 обозначаемое символом
обозначаемое символом 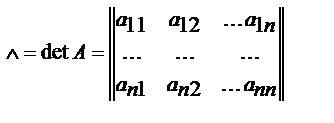
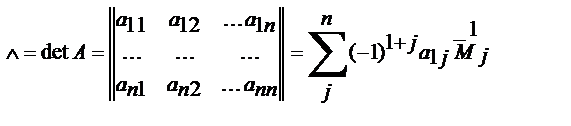


 в силу доказанного выше меняет знак на противоположный, а все остальные величины, стоящие под знаком суммы, совсем не зависят от элементов строк с номерами i1 и i2 и сохраняют свое значение. Тем самым свойство 2°) доказано.
в силу доказанного выше меняет знак на противоположный, а все остальные величины, стоящие под знаком суммы, совсем не зависят от элементов строк с номерами i1 и i2 и сохраняют свое значение. Тем самым свойство 2°) доказано. если
если  для всех j = 1, 2,..., п. Для доказательства разложим каждый из трех определителейпо i-й строке и заметим, что у всех трех определителей все миноры элементов i-й строки одинаковы. Но отсюда следует, что формула
для всех j = 1, 2,..., п. Для доказательства разложим каждый из трех определителейпо i-й строке и заметим, что у всех трех определителей все миноры элементов i-й строки одинаковы. Но отсюда следует, что формула  сразу вытекает из равенств
сразу вытекает из равенств  для всех j = 1, 2,..., п. Следствие 1. Определитель с двумя одинаковыми строками (или столбцами) равен нулю.
для всех j = 1, 2,..., п. Следствие 1. Определитель с двумя одинаковыми строками (или столбцами) равен нулю.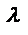 равносильно умножению определителя на это число
равносильно умножению определителя на это число 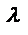 . Следствие 4. Если элементы двух строк (или двух столбцов) определителя пропорциональны, то определитель равен нулю. (В самом деле, в силу следствия 2, множитель пропорциональности можно вынести за знак определителя, после чего останется определитель с двумя одинаковыми строками, который равен нулю согласно следствию 1).
. Следствие 4. Если элементы двух строк (или двух столбцов) определителя пропорциональны, то определитель равен нулю. (В самом деле, в силу следствия 2, множитель пропорциональности можно вынести за знак определителя, после чего останется определитель с двумя одинаковыми строками, который равен нулю согласно следствию 1).
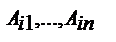 не зависят от элементов i-й строки
не зависят от элементов i-й строки 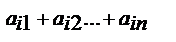 ,то соответствующее равенство является тождеством относительно
,то соответствующее равенство является тождеством относительно 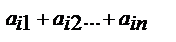 и сохраняется при замене чисел
и сохраняется при замене чисел  , мы получим слева определитель с двумя одинаковыми строками, равный нулю согласно следствию 1. Таким образом,
, мы получим слева определитель с двумя одинаковыми строками, равный нулю согласно следствию 1. Таким образом,  (для любых несовпадающих i u k).
(для любых несовпадающих i u k). тогда det =сумме произведений всевозможных миноров k-го порядка.. det=
тогда det =сумме произведений всевозможных миноров k-го порядка.. det= 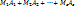 ;
; 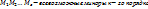 ;
;  Рассмотрим частный случай к=1;
Рассмотрим частный случай к=1;  ;. Следствие 1.
;. Следствие 1. 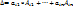 ; Следствие 2. Пусть
; Следствие 2. Пусть  Сумма произведений чисел
Сумма произведений чисел  на алгебраические дополнения соответствующих элементов i-ой строки, определитель
на алгебраические дополнения соответствующих элементов i-ой строки, определитель  равен новому определителю
равен новому определителю  , получающегося из данного дельта заменой i-ой строки на
, получающегося из данного дельта заменой i-ой строки на 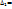
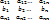 =
=  =
=  . Следствие 3. Сумма произведений всех элементов некоторой строки det алгебраические дополнения соответствующих элементов другой его строки равна нулю.
. Следствие 3. Сумма произведений всех элементов некоторой строки det алгебраические дополнения соответствующих элементов другой его строки равна нулю.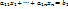

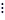 (2)
(2) Ни одно из уравнений не является линейной комбинацией другой строки или столбца. Определитель не равен нулю.. Теорема. Система из n уравнений с n независимыми переменными вида (2) в случае
Ни одно из уравнений не является линейной комбинацией другой строки или столбца. Определитель не равен нулю.. Теорема. Система из n уравнений с n независимыми переменными вида (2) в случае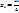 (
( .
.  -определитель матрицы, получаемой системой матрицы, имеет вид
-определитель матрицы, получаемой системой матрицы, имеет вид =
= 

 ……………………. =0
……………………. =0
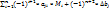 =0. Mi –определитель матрицы, получается при вычеркивании i-ого столбца..
=0. Mi –определитель матрицы, получается при вычеркивании i-ого столбца..  .
. 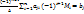 .
.  ..
.. 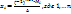 . Набор чисел
. Набор чисел 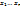 удовлетворяет уравнению j-му. Уравнение
удовлетворяет уравнению j-му. Уравнение 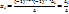 (*)
(*)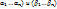 , тогда
, тогда +…+
+…+ 
 (**)
(**) (3)
(3)



 ; 2. Прибавление к строке другой строки; 3. Перестановка строк; 4. Те же самые преобразования для столбцов. Предложение 1. Элементарные преобразования не меняют ранга матрицы. Предложение 2. Элементарные преобразования строк расширенной матрицы соответствуют преобразованию линейных уравнений в эквивалентную систему.
; 2. Прибавление к строке другой строки; 3. Перестановка строк; 4. Те же самые преобразования для столбцов. Предложение 1. Элементарные преобразования не меняют ранга матрицы. Предложение 2. Элементарные преобразования строк расширенной матрицы соответствуют преобразованию линейных уравнений в эквивалентную систему.
 номер первого столбца, не содержащего ноль, если такого нет, то ранг=0, нет базисного минора. Пусть
номер первого столбца, не содержащего ноль, если такого нет, то ранг=0, нет базисного минора. Пусть 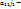 ненулевой элемент. Обозначим, элемент преобразования
ненулевой элемент. Обозначим, элемент преобразования 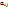 и переставим первую строку на первое место.
и переставим первую строку на первое место.  =
= 
 , где
, где  . Существует
. Существует  -номер столбца, содержащий ненулевой элемент в последней n-1 строке. Произведем в
-номер столбца, содержащий ненулевой элемент в последней n-1 строке. Произведем в 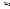 такие же преобразования как и в
такие же преобразования как и в 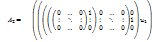 . Продолжим наши преобразования до тех пор, что последняя m-r строк будут состоять из нулей. Предложение 3. При помощи элементарных преобразований строк каждую матрицу размером m*n можно привести можно привести к виду: некоторые r столбцы являются единичными матрицами порядка m, если m-r строк состоят из нулей.
. Продолжим наши преобразования до тех пор, что последняя m-r строк будут состоять из нулей. Предложение 3. При помощи элементарных преобразований строк каждую матрицу размером m*n можно привести можно привести к виду: некоторые r столбцы являются единичными матрицами порядка m, если m-r строк состоят из нулей.
 Ранг матрицы = r, то минор упрощенного вида принмает ранее описанный вид. Приведение к упрощенному виду за счет преобразования строк называется методом Гаусса.. Следствие. Любую квадратную матрицу с ненулевым определтелем, при помощи элемнтарных преобразований, можно превратить в единичную матрицу. Пусть матрица А (m*n), каков бы не был минор при n преобразовании строк матрицы А можем превратить в столбцы единчной матрицы. Rg=r<m, то последнее m-r будут ненулевыми строками. Теорема о базисном миноре. Каждый столбец произвольной матрицы А является линейной комбинацией столбцов, в которых расположен базисный минор. Док-во:
Ранг матрицы = r, то минор упрощенного вида принмает ранее описанный вид. Приведение к упрощенному виду за счет преобразования строк называется методом Гаусса.. Следствие. Любую квадратную матрицу с ненулевым определтелем, при помощи элемнтарных преобразований, можно превратить в единичную матрицу. Пусть матрица А (m*n), каков бы не был минор при n преобразовании строк матрицы А можем превратить в столбцы единчной матрицы. Rg=r<m, то последнее m-r будут ненулевыми строками. Теорема о базисном миноре. Каждый столбец произвольной матрицы А является линейной комбинацией столбцов, в которых расположен базисный минор. Док-во:  (2)соответстующие и связывающие столбцы матрицы не меняются при линейных преобразованиях. (2)-система линейных уравнений. Элементарн. преобр-ния не меняют множ-во её решений, т.е. столбцы матрицы будут удолетворять (2). С простейшими элементарными преобр-ниями столбцы переводят в единичные элементы.
(2)соответстующие и связывающие столбцы матрицы не меняются при линейных преобразованиях. (2)-система линейных уравнений. Элементарн. преобр-ния не меняют множ-во её решений, т.е. столбцы матрицы будут удолетворять (2). С простейшими элементарными преобр-ниями столбцы переводят в единичные элементы.
 Для преобразования матрицы справедлвость теормы очевидно. Для первичной матрицы тетекают те же самые залючения.. Следствие. Каждая строка матрицы есть линейная комбинация строк, в которых расположен базисный минор.
Для преобразования матрицы справедлвость теормы очевидно. Для первичной матрицы тетекают те же самые залючения.. Следствие. Каждая строка матрицы есть линейная комбинация строк, в которых расположен базисный минор.
 (2)
(2)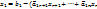 )
)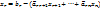
 -элементы преобразованной расширенной матрицы.
-элементы преобразованной расширенной матрицы.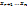 -параметрические неизвестные. Вместе образуют решение системы (6). Опишим ещё один способ. Составим однородную систему уравнений с коэфициентами:
-параметрические неизвестные. Вместе образуют решение системы (6). Опишим ещё один способ. Составим однородную систему уравнений с коэфициентами:

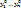 - решение системы, то
- решение системы, то  -также решение системы тогда и только тогда, когда найдется решение приведенной системы
-также решение системы тогда и только тогда, когда найдется решение приведенной системы  , т.ч.
, т.ч. 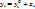 , для
, для 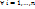 Док-во: Пусть
Док-во: Пусть  - столбцы мат. А,
- столбцы мат. А,  – столбец свободных членов,
– столбец свободных членов,  (8) Пусть
(8) Пусть  (9) Складывая равенства (8) и (9) получим
(9) Складывая равенства (8) и (9) получим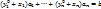 . Т.е. числа (
. Т.е. числа (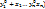 - удовлетворяют системе (1). Пусть (
- удовлетворяют системе (1). Пусть (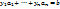 . Вычитая из (9) –(7) имеем
. Вычитая из (9) –(7) имеем 
 -уравнение удовлетворяет системе (7). Терема доказана
-уравнение удовлетворяет системе (7). Терема доказана


